Предлагаемая вниманию читателя книга английского

Предлагаемая вниманию читателя книга английского инженера Р. Тэйлора «Шум» посвящена весьма важной научно-технической проблеме нашего времени: борьбе с шумовым загрязнением окружающей среды. Теперь к жертвам шума следует относить не только котельщиков и клепальщиков, как это было несколько десятков лет назад, но, пожалуй, и каждого жителя города. Год от года шум растет и в домах, и на улице, и на производстве. Например, в Москве и других больших городах за последнее десятилетие шум вырос в 10—15 раз. Ученые уже давно установили, что шум вызывает тугоухость, приводит к нарушениям сна, язвенной болезни, сердечно-сосудистым, нервным и другим заболеваниям. Особенно большой вред шум приносит детям и больным.
Современная акустическая наука может предложить весьма эффективные средства борьбы с шумом, В одних случаях инженеры-акустики умеют снизить чрезмерный шум того или иного механизма, в других — изолировать этот шум, отражая его обратно к месту возникновения и не давая ему распространиться по всему помещению. Если невозможно бороться с самим шумом, с успехом применяют индивидуальные средства защиты человека: ушные заглушки (вкладыши) и противошумные наушники.
К сожалению, несмотря на то что шумовая угроза затрагивает почти все население, борьба с шумом в нашей стране не достигла пока удовлетворительного уровня и не отвечает современным возможностям науки и техники. Конструкторы и изготовители различных механизмов и средств транспорта, а также лица, связанные с их эксплуатацией, еще не уделяют должного внимания охране населения от чрезмерного шума.
Главную причину недостаточного развертывания борьбы с шумом мы видим в отсутствии у соответствующих научно-технических кадров необходимых знаний в области акустики вообще и воздействия шума на человека в частности. Заголовок первой главы («Неведомая наука — акустика») можно адресовать большому кругу лиц, обязанных следить за акустическим климатом.

В деле охраны человека от вредных внешних воздействий акустику используют меньше, чем остальные естественные науки. Это отражается даже в языке: тогда как в популярных книгах и журналах уже не считается нужным пояснять такие слова, как, например, «античастица», «лазер», «хромосома», «мягкая посадка», «жесткое излучение» и т. д., слова: «шумовая проблема», «шумность», «заглушение», «децибелы», «реверберация» и т. п. — часто воспринимаются как какие-то экзотические термины.
Такое положение вещей делает весьма важной пропаганду акустических знаний на популярном уровне. Поэтому появление в переводе настоящей книги, преследующей именно эту цель, следует считать весьма своевременным.
Р. Тэйлор — практический работник в области борьбы с шумом. Он сочетает большой опыт с ясными представлениями о физических процессах — как приводящих к генерации шума современными техническими устройствами, так и лежащих в основе способов противодействия шуму. Книга предназначена в основном для лиц, мало сведущих в акустике. Р. Тэйлору удалось сохранить популярность изложения, несмотря на то что в книге охвачен большой и сложный материал: основы генерации и распространения звука, работа слухового аппарата человека и повреждение слуха шумом, процессы создания шума различными механизмами и устройства для поглощения и изоляции звука; даны сведения об архитектурной и строительной акустике. Кроме того, автор вкратце рассматривает законодательные аспекты борьбы с шумом в Англии, а также приводит некоторые интересные случаи из собственной практики, когда ему сравнительно простыми средствами удавалось существенно улучшить акустические условия в шумных помещениях. Последняя глава книги посвящена «шумовой футурологии». Заключительная фраза книги оптимистична, хотя автор ясно понимает огромный масштаб и сложность задачи обуздания современной тенденции роста окружающего шума.
Тэйлор справедливо отмечает, что борьба с шумом включает, помимо всего прочего, экономический аспект и подчеркивает, что за снижение шума надо «платить» (идет ли речь о денежных затратах или об увеличении массы и габаритов заглушаемого оборудования).

По мнению автора, с которым нельзя не согласиться, подход к современной проблеме шума должен быть всесторонним. Следует учитывать как физико-технические и экономические, так и физиологические стороны вопроса, совершенствовать как способы борьбы с колебаниями воздуха и вибрациями конструкций, так и надлежащие законодательные меры. Необходимость такого подхода показана в книге достаточно ясно и последовательно.
Среди имеющихся отечественных и переводных изданий, посвященных этой теме, нет книги, которая по научному и популяризаторскому уровню приближалась бы к книге Тэйлора. Наибольший практический интерес книга представит для инженерно-технических работников промышленности и транспорта, строителей и градостроителей, сотрудников отраслевых научно-исследовательских институтов и т. д. Книга будет интересна и просто любознательному читателю, особенно если он также является жертвой шума.
М. Исакович.

и критическая частота для различных

Поверхностная плотность и критическая частота для различных материалов
Материал	Объемная плотность, кг/м3•10?3	Модуль Юнга, Н/м2 •10?9	Критическая частота, умноженная на поверхностную плотность, Гц•кг/м2
Свинец	11	14	600 000
Сталь	8	210	98 000
Алюминий	2,7	70	32 000
Стекло	2,5	41	38 000
Бетон	2,3	24	44 000
Кирпичная кладка	2	16	42 000
Твердый картон	0,8	2,1	30 500
Штукатурная плита	0,75	1,9	29 000
Фанера	0,6	4,3	13 200
Флакслинум	0,4	1,2	13 200

Двойная перегородка из гипсовой сухой

Типичные значения звукоизоляции перегородок
	Толщина, мм	Поверхностная плотность, кг/м2	Звукоизоляция, дБ
			Средняя	125 Гц	250 Гц	500 Гц	1 кГц	2 кГц	4 кГц
Фанера	6	3	18	10	13	17	22	24	21
Стекло	5	13	23	17	21	25	26	23	26
Сталь	0,12	9,3	29	20	23	27	32	34	41
Кирпич (оштукатуренный)	145	220	45	34	36	41	51	58	60
Бетон	152	350	47	35	39	45	52	60	67
Двойная перегородка из гипсовой сухой штукатурки с металлическими связями	100	43	43	25	37	44	52	55	45
То же, но с деревянными связями	100	40	40	25	31	40	46	53	48
Фанера, приклеенная по обе стороны деревянных стоек с сечением 25×76 мм	90	12	26	16	18	26	28	37	33
Патентованные модульные акустические панели	76	42	41	24	30	37	41	46	45

на 1000 м3) при комнатной

Типичные значения коэффициента поглощения
Вещество	Коэффициент поглощения, ?
	125 Гц	250 Гц	500 Гц	1 кГц	2 кГц	4 кГц
Воздух ( на 1000 м3) при комнатной температуре				0,03	0.06	0,2
Кирпичная кладка	0,05	0,04	0,02	0,04	0,05	0,05
Бетон	0,02	0,02	0,02	0,04	0,05	0,05
Оконные стекла	0,2		0,1		0,05
Фанера или твердый картон, установленные с воздушным промежутком	0,3		0,15		0,1
Деревянные полы	0,15	0,2	0,1	0,1	0,1	0,1
Тонкий ковер на бетонном полу	0,1	0,15	0,25	0,3	0,3	0,3
Ковер с ворсом на толстом слое войлока	0,1	0,25	0,5	0,5	0,6	0,35
76-миллиметровый слой минеральной шерсти (на жестком основании), облицованный перфорированным металлическим листом	0,4	0,7	0,75	0,9	0,85	0,75
То же для толщины 25 мм (как в акустических плитах)	0,1	0,3	0,6	0,75	0,8	0,8
15-миллиметровые минеральные плиты с щелевой перфорацией (на твердом основании)	0,1	0,25	0,83	0,87	0,64	0.52
12-миллиметровые перфорированные древесноволокнистые плиты	0,2	0,55	0,6	0.6	0,65	0,8

Затухание звука в воздуховодах с акустической облицовкой
Толщина облицовки (минеральная шерсть) на обеих сторонах, мм	Ширина воздушного промежутка, мм	Ослабление на погонные 300 мм, дБ
		125 Гц	250 Гц	500 Гц	1 кГц	2 кГц	4 кГц
25	25	1	2	5	15	37	58
	50	0,5	1	3	10	27	26
	100	—	0,5	2	7	17	10
	200	—	0,5	1	5	7	3
	400	—	—	1	5	2	—
50	25	2	5	11	24	32	48
	50	1	3	9	19	22	28
	100	0,5	2	6	11	12	10
	200	0,5	1,5	3	7	6	2
	400	—	1	2	4	1	—

Шипение, свист, гудение, грохот

Надеюсь, я не слишком разочарую читателя, который уже мнит себя знатоком по части труб с поршнями и пульсирующих баллонов, если скажу ему, что, по всей вероятности, ни те, ни другие ему нигде не встретятся, разве только в какой-нибудь лаборатории. Реальные источники звука гораздо сложнее, чем эти схемы. В книге, посвященной шуму, возможно, и следовало бы начать с пневматических перфораторов и сверхзвуковых самолетов, но, соблюдая последовательность, мы в первую очередь остановимся на некоторых простых звуковых «машинах», применение которых не ограничено рамками лабораторий. В этих устройствах происходит большинство процессов образования шумов, которые так нам досаждают. Речь пойдет о музыкальных инструментах. В них применены наилучшие способы создания звуков, и, познакомившись с ними, мы по крайней мере будем знать, чего следует избегать при конструировании различных механизмов.

Музыкальные инструменты, как и многие другие источники звука, можно разбить на три группы: инструменты, звучание которых обусловлено аэродинамическими процессами, инструменты, создающие звук путем поддержания незатухающих механических колебаний, и инструменты, звучащие при ударе или при соударении тел. Все они могут служить прекрасными объектами для нашего исследования. Музыкальные инструменты из деликатности почти никогда не причисляют к источникам шума, а их тщательно разработанная конструкция исключает создание каких бы то ни было звуков, кроме предусмотренных певучих звучаний. Кроме того, при игре на музыкальных инструментах почти всегда стремятся к их гармоничному созвучию. У каждого музыкального инструмента найдутся двойники среди шумящих машин.

Рис. 5. Блок-флейта (в разрезе).

Примерами инструментов первой группы (издающих звуки аэродинамически) могут служить некоторые духовые инструменты, в частности блок-флейта (продольная флейта, или рекордер) и диапазонные органные трубы. Произвести звук без подачи энергии невозможно. Мы уже видели, что звук — это просто способ передачи энергии сквозь воздух или какую-либо другую среду в виде волн давления, в которых энергия непрерывно и быстро переходит из одной формы в другую: из потенциальной в кинетическую и обратно.

При колебании поршня в трубе энергию поставлял вращающийся коленчатый вал, в случае пульсирующего баллона — насос. В духовой инструмент энергию подает сам музыкант, который давлением своих легких вдувает в него модулированную струю воздуха. На рис. 5 изображена блок-флейта. Воздух, сжатый в легких, вдувается через узкую щель мундштука и выходит из него в виде короткой струи; при этом то по одну, то по другую сторону от струи образуются вихри. Они возникают потому, что по обе стороны от быстро движущегося потока воздуха давление падает. Это можно увидеть, например, если дунуть на монетку, лежащую на столе: монетка перевернется. Падение давления вызывает отсасывание струи с боков; поэтому большая скорость воздуха, выходящего из мундштука, и турбулентность струи приводят к образованию вихрей. Затем эти вихри сталкиваются с клиновидным выступом амбушюра флейты и проходят сверху или снизу выступа. Практически именно положение этого выступа определяет частоту образования вихрей: чем меньше расстояние от отверстия мундштука до выступа, тем чаще образуются вихри. Точно так же, чем сильнее дует музыкант, тем больше скорость воздушной струи и частота образования вихрей.

Образование вихрей и прохождение их то по одну, то по другую сторону от клиновидного выступа вызывает колебания давления в ближайших слоях воздуха. Если распилить блок-флейту сразу же позади выступа, издаваемый ею звук окажется весьма немузыкальной смесью из шипения и свиста, и его высота будет зависеть от силы, с которой музыкант дует в мундштук. В этом случае колебания давления далеко не такие простые, как при пульсациях баллона, но принцип возникновения звука тот же. Расширяясь и сжимаясь, баллон сжимает и разрежает окружающий сферический слой воздуха; это вызывает колебания давления, передаваемые во всех направлениях от одного слоя к другому со скоростью звука. Различие между баллоном и отпиленным мундштуком блок-флейты состоит в том, что последний производит сжатия и разрежения не путем колебания поверхности, а в результате колебаний самого воздуха и что возникающие при этом волны не имеют правильной сферической формы.

Почему мы отпилили мундштук от нашей блок-флейты? Только потому, что остальная часть инструмента не имеет никакого отношения к созданию звука, а только видоизменяет звук, возникающий в мундштуке. Если закрыть отверстия в стенке корпуса инструмента, он будет напоминать трубу, в которой ходит поршень. Но в предыдущей главе мы опустили одно важное обстоятельство, касающееся поведения такой трубы с поршнем. Предполагалось, что волны сжатия, бегущие вдоль трубы, исчезают, добежав до ее конца. В действительности это вовсе не так. Когда звуковая волна достигает открытого конца трубы, она внезапно встречает бесконечный объем воздуха в неограниченном наружном пространстве. Ничтожный объем воздуха, который волна переместит из узкой трубы в наружное пространство, не в состоянии повысить давление снаружи и поэтому волна не сможет выйти наружу, а, отразившись от открытого конца трубы, побежит в обратную сторону. Явление отражения звука играет важнейшую роль в акустике, и мы рассмотрим его гораздо подробнее в дальнейшем.

Отраженная волна бежит обратно по трубе. В блок-флейте она вскоре наталкивается на мундштук, где снова отражается, опять бежит вперед, и этот процесс последовательных отражений продолжается, причем звуковая энергия почти полностью остается внутри трубы, и при каждом отражении теряется лишь малая ее часть.

Рис. 6. Прямая (а) и отраженная (б) волны.

На рис. 6, а показано распределение давлений в исходной волне для последовательных моментов времени t1, t2 ... t8, показывающее перемещение волны вдоль трубы в течение одного периода. На рис. 6, б изображено перемещение в обратную сторону первой отраженной волны для тех же моментов времени. Обе волны существуют в трубе одновременно, накладываясь одна на другую. Чтобы получить результирующую картину, волны следует сложить согласно принципу суперпозиции. При этом выясняется нечто удивительное: в результате никакого движения волн ни в одну, ни в другую сторону не получается — образуется одна стоячая волна (рис. 7).

В такой стоячей волне распределение звукового давления уже не перемещается ни вправо, ни влево: в каждой точке звуковое давление изменяется периодически, с различными амплитудами для разных точек. Например, в точке A амплитуда волны всегда равна нулю, а в точке В всегда максимальна. А в бегущей волне изменения давления имели одинаковую амплитуду во всех точках и давление достигало одного и того же максимума, хотя и в разные моменты времени и различных точках по длине трубы. После первого отражения наступает второе и т. д., и волна, подобно челноку, продолжает бегать вперед-назад, и отражения, складываясь, увеличивают амплитуду стоячей волны, пока более ранние отражения не затухнут в результате поглощения звуковой энергии.

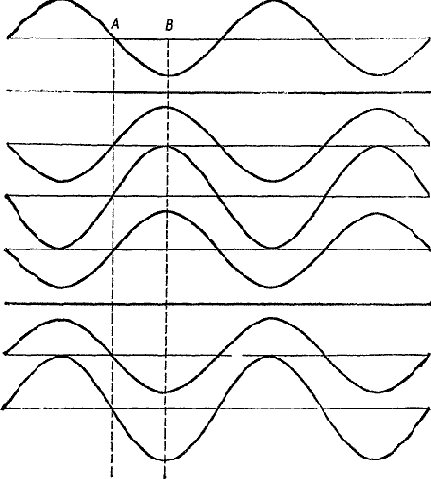Рис. 7. Стоячая волна — сумма бегущих волн, показанных на рис. 6.

Взглянув снова на график стоячей волны, мы обнаружим еще одно существенное обстоятельство: на открытых концах трубы всегда оказываются минимумы (нулевые значения) амплитуды. Следовательно, вдоль трубы всегда должно уложиться целое число полуволн звука. Тогда, действительно, в результате последовательных отражений амплитуда стоячей волны достигает значительной величины: происходит резонанс. При резонансе отраженные волны комбинируются так, что усиливают друг друга — это так называемая конструктивная интерференция волн. Если же на длине трубы не укладывается целое число длин волн, то последовательные отражения уже не будут усиливать друг друга; максимумы одних волн придутся на минимумы других, и в итоге получится стоячая волна малой амплитуды. Резонанс в этом случае отсутствует, и говорят о деструктивной интерференции волн.

Теперь откроем отверстия в стенке блок-флейты. Мы видели, что стоячие волны возникают в результате отражения волны от обоих концов трубы; отражение происходит благодаря внезапности столкновения волны со свободным наружным воздухом. Если открыть отверстие, то такое же отражение возникнет уже ближе к началу блок-флейты, звуковая волна столкнется с наружным воздухом несколько раньше, эффективная длина трубы уменьшится, а значит, ее резонансная частота возрастет.

Снова приложим мундштук к корпусу блок-флейты и подуем в него. Каждый, кто пробовал играть на духовых инструментах, знает, что не всегда достаточно взять мундштук в рот и подуть, чтобы получить желаемый звук, на который рассчитывал изготовивший инструмент мастер. Пусть при всех закрытых отверстиях дискантовая блок-флейта издает звук F (фа) выше среднего C (до). Если только выступ амбушюра находится в правильном положении, то частота возникновения вихрей, о которых говорилось выше, будет зависеть от силы, сообщаемой воздушной струе. При закрытых отверстиях корпус блок-флейты представляет собой трубу, резонирующую на частоте 349 Гц. Опытный флейтист дует с силой, необходимой для формирования примерно 349 вихрей в секунду; поэтому возникающие колебания давления вызовут колебания воздуха в корпусе блок-флейты почти так же, как это происходило при движении поршня в трубе. Будучи резонатором, корпус блок-флейты усиливает каждую бегущую вдоль него волну с частотой 349 Гц и длиной чуть меньше одного метра.

Самой низкой частоте резонанса закрытой трубы соответствует длина волны звука, вдвое большая, чем длина трубы. В нашем частном случае длина инструмента должна быть чуть меньше 0,5 м. Резонанс в трубе обеспечивает обратную связь и вызывает образование вихрей точно в такт с резонансной частотой, если только флейтист не дует слишком сильно или слишком слабо. Когда отверстия в корпусе инструмента открыты, резонансная частота возрастает, но в остальном процесс протекает так же; флейтист подсознательно варьирует силу, с которой он дует, таким образом, чтобы ускорить образование вихрей, чему способствует и действие обратной связи. Если он будет дуть слишком сильно, то прежде всего слегка увеличится частота звука, издаваемого блок-флейтой, потому что, когда частота образования вихрей близка, но несколько превышает резонансную частоту корпуса, результирующая частота резонанса равна среднему между ними.

Если флейтист подует еще сильнее, блок-флейта протестующе взвизгнет (в действительности все происходящее сложнее, и в этой главе мы еще вернемся к данному вопросу).

Рассмотрим теперь вторую группу музыкальных инструментов и попробуем сравнить их с блок-флейтой. К этой группе относится семейство скрипок; скрипка позволяет познакомиться со многими возможными механизмами образования шума.

Как это ни странно, но легче всего непосредственно сравнить между собой принципы действия скрипки и блок-флейты, хотя они и относятся к разным группам музыкальных инструментов Струны скрипки можно уподобить корпусу блок-флейты, то есть резонирующей трубе. В такой трубе исходное возмущение создается на одном ее конце, но это не обязательно: возмущение можно вызывать в любой точке внутри трубы Натянутая струна также способна резонировать. В этом легко убедиться, если дернуть натянутую резиновую ленточку Правда, громкого звука при этом не получится, потому что ленточка слишком тонка и не способна создать значительные колебания в окружающем воздухе Как показано на рис. 8, при отклонении струны воздух не сжимается, а обтекает струну. Но это побочное обстоятельство, и оно не снижает значения того факта, что струна обладает резонансными свойствами.

Вспомним, что основной физический процесс при распространении звуковой волны, — это непрерывный переход кинетической энергии в потенциальную и обратно То же самое происходит и при колебании струны: когда струну дергают, отклоняя ее в одну сторону, она растягивается и приобретает потенциальную энергию; когда струну отпускают, сила натяжения стремится вернуть ее в положение равновесия, струна приобретает кинетическую энергию и импульс и, минуя по инерции положение равновесия, отклоняется в другую сторону, то есть снова в положение, в котором струна имеет потенциальную энергию, и т. д. Такие колебания совершаются до тех пор, пока струна не истратит всю энергию, сообщенную ей при оттягивании.

Впрочем, существует и другой, более научный подход к колебанию струны, позволяющий выявить сходство струны с трубой Если взять очень длинную слабонатянутую струну и ущипнуть ее у одного конца, то созданное щипком смещение побежит вдоль струны, подобно звуковой волне в длинной трубе И точно так же, достигнув конца струны, смещение отразится и побежит в обратную сторону. Если вместо однократного щипка непрерывно возбуждать колебания струны, отраженная волна будет накладываться на исходную и струна будет выглядеть подобно подвижному графику стоячей волны в трубе. Учитывая последовательные отражения от обоих концов струны, можно понять, каким образом струна совершает резонансные колебания такие, как воздух в трубе, с тем отличием, что пучности и узлы соответствуют не точкам большого и малого давления, как в трубе, а точкам максимального и нулевого смещений. Резонансная частота струны также обратно пропорциональна ее длине.

Рис. 8. Обтекание воздухом колеблющейся струны.

Подобно тому как можно варьировать резонансную частоту трубы, изменяя плотность или упругость газа, ее заполняющего, и таким образом изменяя скорость звука, а следовательно, длину звуковой волны, можно варьировать и резонансную частоту струны. Аналогия состоит в том, что, увеличивая массу струны или уменьшая ее натяжение при постоянной длине струны, можно уменьшить ее резонансную частоту, и наоборот В этой возможности не отдавали себе отчета до XVII в., что чрезвычайно задержало появление современного фортепьяно. Для того чтобы сохранить диапазон в семь с половиной октав, которым располагает современный инструмент, рояль со струнами, обладающими одинаковой погонной плотностью и равным натяжением, должен был бы иметь длину более 12 м.

В скрипке аналогом образования вихрей в блок-флейте служит колебание струны, создаваемое движением смычка, натертого канифолью, поперек струн. При звучании какого-либо тона здесь также имеет место действие обратной связи, подгоняющее частоту колебания струны под смычком к частоте прозвучавшего тона.

К сожалению, играть на скрипке — это не значит просто держать ее под подбородком и водить по ее струнам смычком. Но теперь нам уже легче понять, почему начинающий скрипач извлекает из своего инструмента столь душераздирающие звуки: если исходное возмущение, вызываемое в струнах смычком, не достаточно точно совпадает с резонансной частотой струны (а такое совпадение зависит от давления на струны и скорости движения смычка), то результирующий звук будет очень сходен с визгом блок-флейты, в которую дуют с излишней силой.

Как уже упоминалось, сами по себе струны не могут издавать сильных звуков. Однако они колеблются весьма энергично. Струна обладает энергией, и ее движение имеет колебательный характер, что достаточно для создания звука, но передача звука от струн в воздух очень мала. Это затруднение устраняет корпус скрипки: через подставку колебания струны передаются деревянному корпусу, который действует как наш воображаемый пульсирующий баллон, с той разницей, что звуковые волны создаются не только снаружи, но и внутри корпуса. Корпус усиливает передачу звука в воздух, так как на воздух воздействует поверхность гораздо большая, чем поверхность струны. Звуковые волны, возникающие внутри корпуса, комбинируются друг с другом, но скрипичный мастер должен рассчитать корпус таким образом, чтобы резонансная частота внутреннего объема скрипки была ниже частоты самой низкой ноты любой струны, иначе какая-то из нот будет доминировать над остальными. Иногда мастеру это не удается, и тогда у скрипки появляется так называемый «волчий тон». Резонансы — бич плохих скрипок.

Перейдем к третьей группе инструментов — инструментам, работающим от удара или соударений тел. В голову сразу приходит мысль о медных тарелках оркестра и барабанах. В качестве примера рассмотрим тарелки. Барабаном мы займемся отдельно в главе 8. У тарелки много общего с колеблющейся струной. Теоретически струна, совершающая колебания, представляет собою одномерную систему: нас интересуют только длина ее и расстояние, на которое она отклоняется от положения равновесия.

Во многих отношениях тарелку можно рассматривать как двумерную струну. Заставить струну колебаться можно не только скольжением смычка, но и щипком или ударом. То же можно сказать и о тарелке, хотя вряд ли нам когда-либо придется увидеть, как играют смычком на тарелке; но клоуны, которые извлекают музыкальные звуки из стальной пластинки, водя по ее краю смычком («поющая пила»), — заурядный номер цирковой программы.

Если ударить по медной тарелке, в металле побегут изгибные волны, которые отразятся от краев, подобно тому как отражаются волны в струне. Разумеется, тарелка не находится в состоянии натяжения, но роль натяжения играет упругость металла. Тарелка гораздо успешнее, чем струна излучает звук в воздухе; это обусловлено ее большой плоской поверхностью: ведь только по краям тарелки воздух может обогнуть ее и не подвергнуться сжатию или разрежению.

Существует еще один очень важный аспект генерации звука, которого мы пока не касались. Мы уже выяснили, что такое звук, как он создается и как его можно усилить; мы рассмотрели блок-флейты, скрипки и тарелки, сравнили их друг с другом, но не объяснили, почему звуки, извлекаемые из них, лишены даже отдаленного сходства. Эти инструменты представляют собой превосходные примеры «механизмов», производящих звук; подобные механизмы можно обнаружить в любой шумной машине. И все-таки, сколько бы скрипок ни играло одновременно, пусть даже как угодно плохо и громко, они никогда не будут звучать так, как пневматическое сверло!

Рис. 9. Расположение узлов (У) и пучностей (П) в резонирующих трубах
(ряд можно продолжать бесконечно).

Чтобы объяснить, почему это происходит, вернемся к колеблющейся струне, закрепленной для лучшей слышимости звука на резонансной деке. Если осторожно прикоснуться к середине колеблющейся струны, издаваемый ею звук повысится на октаву. На первый взгляд кажется, что причина такого повышения очевидна — мы вдвое уменьшили длину струны, следовательно, вдвое снизили длину волны и удвоили частоту звука.

Однако правильное объяснение таково: приложив палец к струне, мы остановили ее колебание с основной, или резонансной, частотой, и при этом обнаружилось, что все время струна колебалась с множеством еще и других частот; эти другие колебания называют обертонами или гармониками. Все приводимые раньше примеры были в той или иной мере искусственными, потому что очень редко создается звук, состоящий только из одной частоты. Как мы уже видели, трубы и струны резонируют на частотах, определяемых их длиной, потому что на концах трубы или струны всегда должен оказаться узел или пучность. Однако узлы или пучности придутся на концы трубы или струны и при частотах, кратных основной частоте; при этом только увеличится общее число узлов и пучностей (рис. 9). Следовательно, и на этих кратных частотах также возможны резонансные колебания. Действительно, каждая музыкальная нота, за редким исключением, состоит не только из своей основной частоты, но еще из довольно большого числа гармоник, или гармонических составляющих. Каждый музыкальный инструмент создает звуки своего определенного тембра (или окраски), что обусловлено различием в числе обертонов или относительной величине их амплитуд. Иногда эти различия возникают не только из-за наличия многих резонансов в воздушном столбе или в струне, но также и в результате резонансных колебаний корпуса инструмента. Дерево не легко приходит в состояние интенсивных колебаний, так как энергия колебаний быстро растрачивается в результате внутреннего затухания. Поэтому делать колокола из дерева бессмысленно, а звук деревянных духовых инструментов не особенно сильно окрашен, так как корпус инструмента не вносит сколько-нибудь заметного вклада, и кроме того, шероховатость внутренней поверхности деревянного инструмента значительно большая, чем, например, у медных труб, способствует затуханию высоких обертонов, придающих звуку яркость и даже резкость.

Свойства меди как бы обратны свойствам дерева, поэтому для отливки колоколов обычно применяют бронзу.

В медных духовых инструментах твердая, гладкая внутренняя поверхность сохраняет в результирующем звуке большую часть гармоник. Сурдина, надеваемая на медную трубу, приглушает ряд гармоник и смягчает тембр. Применяют сурдину и для скрипки, укрепляя зажим на подставке, что вводит трение в колебательное движение струн и сообщает тону мягкость и серебристость. Подробнее о затухании и поглощении звука мы будем говорить в следующих главах.

Благодаря наличию лишнего измерения набор гармоник у медных тарелок значительно сложнее, чем у струн или труб. В тарелке гораздо богаче возможности взаимного расположения узлов и пучностей; геометрия тарелок приводит к возникновению множества резонансов с близкими частотами, благодаря чему тарелки обладают очень красочным, но отнюдь не мелодичным звучанием.

Теперь уже совершенно ясно происхождение высоких по тону писков и визгов, которые издают некоторые инструменты, когда в них слишком сильно дуют или слишком быстро водят смычком по их струнам. Частота исходных возмущений становится слишком высокой для возбуждения основной частоты резонатора, и вместо нее возбуждается одна из гармоник. Однако это же явление можно применить с пользой: на нем основано действие инструментов семейства горнов. Играя на горне, музыкант может вызвать звук основной частоты (иногда называемой первой гармоникой) или, напрягая губы, колебание которых заменяет образование вихрей в блок-флейте, может заставить звучать вторую, третью или множество других гармоник; так как по высоте звука низкие гармоники разделены большими интервалами (рис. 10), на таком инструменте, как горн, трудно сыграть что-нибудь более сложное, чем песенка «Бери ложку, бери хлеб», содержащую преимущественно интервалы в квинту и кварту. Играя на трубе, это затруднение можно обойти, потому что труба практически состоит как бы сразу из трех горнов с общими мундштуком и раструбом, но с корпусами различной длины, которые можно открывать и закрывать, пользуясь клапанами.

Благодаря этому на трубе можно получить значительно большее число гармоник.

Рис. 10. Музыкальная нотация гармоник (натуральная темперация).
Частоты гармоник равны основной частоте, умноженной на 2, 3, 4 и т. д.

В отношении нумерации гармоник существует известная путаница: музыканты в отличие от акустиков иногда называют вторую гармонику первой, третью — второй и т д, но в этой книге первая гармоника — это всегда основная частота, и счет гармоник начинается с нее.

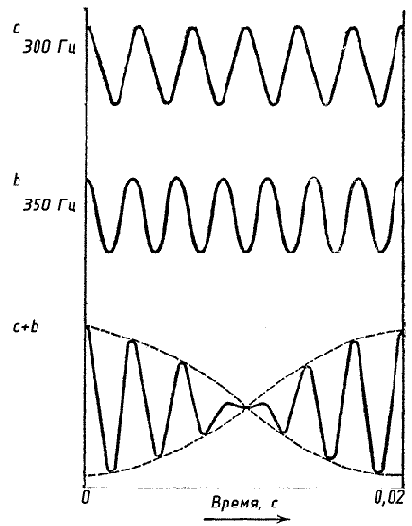Рис. 11. Наложение звуков.

До сих пор речь шла только о приятных звуках, а также о различных инструментах, производящих их, но на свете не так много мелодичных или гармоничных звуков. Почему? Что такое гармония и что такое диссонанс? Что делает музыку приятной, а шум — неприятным? Мы видели, что у музыкального звука большая часть энергии приходится на основную частоту и меньшая часть — на остальные гармоники. Когда две одинаковые ноты звучат одновременно, то колебания могут не совпадать по фазе, но сочетание звуков остается совершенно регулярным, потому что оба звука вызывают колебания давления, следующие друг за другом точно с одинаковой частотой. Если же частота одной из нот увеличится, допустим с 300 Гц до 350 Гц, новое сочетание будет составлять две ноты, из которых одна соответствует 300, а вторая — 350 колебаниям в секунду. Колебания будут происходить так, как показано на рис. 11, и в нашем случае два звука будут усиливать друг друга только 50 раз в секунду, то есть с частотой 50 Гц, численно равной разности между частотами этих нот. Несмотря на то что этот так называемый разностный тон может и не восприниматься сознательно, все же образуется некоторая третья нота частотой 50 Гц. Именно присутствие этого третьего пульсирующего звука и придает комбинации данных нот диссонансное звучание[10]. И действительно, когда сюда же присоединяются еще и гармоники обеих нот и их разностные тоны — толкотня получается изрядная!

Посмотрим, что произойдет, если частота второй ноты вдвое больше частоты первой ноты, иначе говоря, интервал между ними составляет одну октаву. Теперь частоты наших нот равны соответственно 300 и 600 Гц, и разностный тон также имеет частоту 300 Гц. Следовательно, его частота равна частоте первой ноты, и он сольется с ней так же хорошо, как соединяются ноты, равные по частоте. Вот почему октава представляет собой такой гармоничный интервал — самый гармоничный из возможных. Так же гармонично будут сливаться и гармоники с их разностными тонами. Следующий наиболее гармоничный интервал — квинта, в этом случае частота одной ноты на 50 % выше, чем другой, и разностный гон оказывается точно на октаву ниже более низкой из нот.

Действительно резкое неблагозвучие возникает из набора множества разностных тонов в том случае, когда исчезает упорядоченная зависимость между отдельными нотами и остаются только пульсирующие звуки «кошачьего концерта». Если, например, нажать две самые нижние педали 16-футового регистра органа, получится превосходная имитация шума судового дизельного двигателя. Диссонанс, по существу, проблема количественная, он определяется интенсивностью биений, образующих разностные тоны Специалистам по электронике, знакомым с принципом гетеродинирования сигналов в радиосвязи, сущность этой проблемы должна быть понятна.

Рис. 12. Формы волн для свиста и гула.

Мы не коснулись еще одного очень распространенного типа звуков, который также представляет значительный интерес. Все музыкальные инструменты и даже дизельный двигатель производят звуки с периодически повторяющейся формой волны. Но нерегулярные, случайные и совсем не повторяющиеся звуковые волны встречаются столь же часто, как и периодические. Прислушаемся к ветру, к шелесту листьев, к шуму прибрежных волн, разбивающихся о берег, наконец, к реву форсунки парового котла, работающего на жидком топливе. В этих звуках нет ни нот, ни гармоник, ни гармонии, ни диссонанса.

Появляются такие звуки в результате турбулентности того или другого рода, а турбулентность — это просто беспорядочное движение, кружение и завихрение среды. При этом возникают колебания давления, которые вызывают в воздухе волны сжатия так же, как и любой источник звука, но без правильного повторения или ритмического движения. Случайный шум может возникать и как следствие других явлений, например в результате трения о неровную поверхность.

Как бы то ни было, но из нерегулярности шума отнюдь не следует, что к нему не применимо понятие частоты. Очевидно, шипение — звук более высокого тона, чем грохот, хотя оба они носят случайный характер. Основана эта разница на том, что колебания давления при шипении происходят гораздо чаще, чем при грохоте. Это хорошо видно из рис. 12. Но и шипение, и грохот по своему звучанию совершенно отличны от периодических или гармонических звуков, и это обусловлено тем, что ухо не получает возбуждения в той упорядоченной форме, которая создает ощущение отдельных нот. Из-за отсутствия определенных гармоник различные звуки шипения лишены своеобразия и очень сходны между собой.

Когда мы имеем дело с шумом механизмов, основу звука, который мы слышим, составляет именно беспорядочный шум. К нему часто присоединяются чистые тоны и их гармоники, нередко в диссонансных сочетаниях, и в результате образуется звуковая волна очень сложной формы, содержащая периодические компоненты, наложенные на беспорядочный фон.

&nbsp

[10] Здесь автор допускает неточность: в данном случае никакого разностного тона не получается, а разностная частота 50 Гц есть частота следования биений (пульсаций интенсивности звука), образующихся при совместном действии двух близких тонов. — Прим. ред.

Шум вдецибелах

В наше время все уже что-то слышали о «децибелах», но почти никто не знает, что это такое. Децибел представляется чем-то вроде акустического эквивалента «свечи» — единицы силы света — и кажется связанным со звоном колокольчиков[11]. Однако это совсем не так: свое название децибел получил в честь Александера Грейама Белла — изобретателя телефона.

Децибел не только не единица измерения звука, он вообще не является единицей измерения, во всяком случае в том смысле, как, например, вольты, метры, граммы и т. д. Если угодно, в децибелах можно измерить даже длину волос, чего никак нельзя сделать в вольтах. По-видимому, все это звучит несколько странно, так что попытаемся дать разъяснение. Вероятно, никто не удивится, если я скажу, что расстояние от Лондона до Инвернесса в двадцать раз больше, чем от моего дома до Лондона. Я могу выразить любое расстояние, сравнивая его с расстоянием от моего дома до Лондона, скажем до площади Пикадилли Расстояние от Лондона до Джон-о'Тротса в двадцать шесть раз больше, чем это последнее расстояние, а до Австралии — в 500 раз. Но это не означает, что Австралия удалена от чего бы то ни было на 500 единиц. Все приведенные числа выражают только отношения величин.

Одна из измеримых характеристик звука — это количество заключенной в нем энергии; интенсивность звука в любой точке можно измерить как поток энергии, приходящейся на единичную площадку, и выразить, например, в ваттах на квадратный метр (Вт/м2). При попытке записать в этих единицах интенсивность обычных шумов сразу же возникают трудности, так как интенсивность наиболее тихого звука, доступного восприятию человека с самым острым слухом, равна приблизительно 0,000 000 000 001 Вт/м2. Один из наиболее громких звуков, с которым мы сталкиваемся уже не без риска вредных последствий, — это шум реактивного самолета, пролетающего на расстоянии порядка 50 м.

Его интенсивность составляет около 10 Вт/м2. А на расстоянии 100 м от места запуска ракеты «Сатурн» интенсивность звука заметно превышает 1000 Вт/м2. Очевидно, что оперировать числами, выражающими интенсивности звука, лежащие в столь широком диапазоне, очень трудно, независимо от того, представляем ли мы их в единицах энергии или даже в виде отношений. Существует простой, хотя и не вполне очевидный выход из данного затруднения. Интенсивность самого слабого слышимого звука равна 0,000 000 000 001 Вт/м2. Математики предпочтут записать это число таким образом: 10?12 Вт/м2. Если кому-либо такая запись непривычна, напомним, что 102 это 10 в квадрате, или 100, а 103 это 10 в кубе, или 1000. Аналогично 10?2 означает 1/102, или 1/100, или 0,01, а 10?3 это 1/103, или 0,001. Умножить любое число на 10x — значит х раз умножить его на 10.

Пытаясь найти наиболее удобный способ выражения интенсивностей звука, попробуем представить их в виде отношений, приняв за эталонную интенсивность величину 10?12 Вт/м2. При этом будем отмечать, сколько раз нужно умножить эталонную интенсивность на 10 для того, чтобы получить заданную интенсивность звука. Например, шум реактивного самолета в 10 000 000 000 000 (или в 1013) раз превышает наш эталон, то есть этот эталон необходимо 13 раз умножить на 10. Такой способ выражения позволяет значительно уменьшить значения чисел, выражающих гигантский диапазон звуковых интенсивностей; если мы обозначим однократное увеличение в 10 раз как 1 бел, то получим «единицу» для выражения отношений. Так, уровень шума реактивного самолета соответствует 13 белам. Бел оказывается слишком большой величиной; удобнее пользоваться более мелкими единицами, десятыми долями бела, которые и называют децибелами. Таким образом, интенсивность шума реактивного двигателя равна 130 децибелам (130 дБ), но во избежание путаницы с каким-либо другим эталоном интенсивности звука следует указать, что 130 дБ определяется относительно эталонного уровня 10?12 Вт/м2.

Если отношение интенсивности данного звука к эталонной интенсивности выражается каким-нибудь менее круглым числом, например 8300, перевод в децибелы окажется не таким простым. Очевидно, число умножений на 10 будет больше 3 и меньше 4, но для точного определения этого числа необходимы длительные вычисления. Как обойти такое затруднение? Оказывается, весьма просто, поскольку все отношения, выраженные в единицах «десятикратных увеличений», давно вычислены — это логарифмы.

Любое число можно представить как 10 в какой-то степени: 100 это 102 и, следовательно, 2— это логарифм 100 при основании 10; 3 — логарифм 1000 при основании 10 и, что менее очевидно, 3,9191 — логарифм 8300. (Нет необходимости все время повторять «при основании 10», потому что 10 — самое распространенное основание логарифма, и если нет другого указания, то подразумевается именно это основание. В формулах эта величина записывается как log10 или lg.)

Пользуясь определением децибела, можем теперь записать уровень интенсивности звука в виде:

Например, при интенсивности звука в 0,26 (2,6×10-1) Вт/м2 уровень интенсивности в дБ относительно эталона 10?12 Вт/м2 равен

Но логарифм 2,6 равен 0,415; следовательно, окончательный ответ выглядит так:

10 × 11,415 = 114 дБ

(с точностью до 1 дБ).

Не следует забывать, что децибелы не являются единицами измерения в том смысле слова, как, например, вольты или омы, и что соответственно с ними приходится обращаться иначе. Если две аккумуляторные батареи по 6 В (вольт) соединить последовательно, то разность потенциалов на концах цепи составит 12 В. А что получится, если к шуму в 80 дБ добавить еще шум в 80 дБ? Шум общей интенсивностью в 160 дБ? Никак нет — ведь при удвоении числа его логарифм возрастает на 0,3 (с точностью до двух десятичных знаков). Тогда при удвоении интенсивности звука уровень интенсивности увеличивается на 0,3 бела, то есть на 3 дБ.

Это справедливо для любого уровня интенсивности: удвоение интенсивности звука приводит к увеличению уровня интенсивности на 3 дБ. В табл. 1 показано, как увеличивается уровень интенсивности, выраженный в децибелах, при сложении звуков различной интенсивности.

Теперь, разрешив тайну децибела, приведем несколько примеров. В табл. 2 даны перечень типичных шумов и уровни их интенсивности в децибелах.

Таблица 1
Сложение уровней интенсивности звука (точность ±0,5 дБ)
Разность между двумя уровнями, дБ	Прибавка к более высокому уровню
0	3
1	2,5
2	2
3	2
4	1,5
5	1
6	1
7	1
8	0,5
9	0,5
10	0

Таблица 2
Интенсивность типичных шумов
Примерный уровень звукового давления, дБА	Источник звука и расстояние до него
160	Выстрел из ружья калибра 0,303 вблизи уха
150	Взлет лунной ракеты, 100 м
140	Взлет реактивного самолета, 25 м
120	Машинное отделение подводной лодки
100	Очень шумный завод
90	Тяжелый дизельный грузовик, 7 м Дорожный перфоратор (незаглушенный), 7 м
80	Звон будильника, 1 м
75	В железнодорожном вагоне
70	В салоне небольшого автомобиля, движущегося со скоростью 50 км/ч; квартирный пылесос, 3 м
65	Машинописное бюро Обычный разговор, 1 м
40	Учреждение, где нет специальных источников шума
35	Комната в тихой квартире
25	Сельская местность, расположенная вдали от дорог

Каким образом можно определить интенсивность данного звука? Это довольно сложная задача; значительно легче измерить колебания давления в звуковых волнах. В табл. 3 приведены значения звукового давления для звуков различной интенсивности. Из этой таблицы видно, что диапазон звуковых давлений не так широк, как диапазон интенсивностей: давление возрастает вдвое медленнее, чем интенсивность. При удвоении звукового давления энергия звуковой волны должна увеличиться в четыре раза — тогда соответственно увеличится скорость частиц среды. Поэтому, если мы измерим звуковое давление, как и интенсивность, в логарифмическом масштабе и, кроме того, введем множитель 2, получим те же величины для уровня интенсивности.

Например, звуковое давление самого слабого из слышимых звуков равно примерно 0,00002 Н (ньютона)/м2, а в кабине дизельного грузовика оно составляет 2 Н/м2, следовательно, уровень интенсивности шумов в кабине равен

Таблица 3
Интенсивность, звуковое давление и уровень звука в воздухе при комнатной температуре и нормальном давлении на уровне моря
Интенсивность, Вт/м2	Звуковое давление, Н/м2	Уровень звука, дБ

Выражая уровень звукового давления в децибелах, следует помнить, что при увеличении давления вдвое прибавляется 6 дБ. Если в кабине дизельного грузовика шум достигнет 106 дБ, то звуковое давление удвоится и составит 4 Н/м2, а интенсивность увеличится в четыре раза и достигнет 0,04 Вт/м2.

Мы много говорили о мере интенсивности звука, но совершенно не касались практических методов измерения этой величины. К доступным для измерения характеристикам звуковой волны относятся интенсивность, давление, скорость и смещение частиц. Все эти характеристики непосредственно связаны друг с другом, и, если удается измерить хотя бы одну из них, остальные можно вычислить.

Нетрудно увидеть или почувствовать на ощупь колебание легких предметов, оказавшихся на пути звуковой волны. На этом явлении основан принцип действия осциллографа — самого старого вида шумомера. Осциллограф состоит из диафрагмы, к центру которой прикреплена тонкая нить, механической системы для усиления колебаний, и пера, записывающего на бумажной ленте смещения диафрагмы. Такие записи напоминают «волнистые линии», о которых мы говорили в предыдущей главе.

Этот прибор был крайне малочувствителен и годился только для подтверждения акустических теорий ученых того времени. Инерция механических деталей предельно ограничивала частотную характеристику и точность прибора. Замена механического усилителя оптической системой и использование фотографического метода регистрации сигналов позволили значительно снизить инерционность прибора.

В усовершенствованном таким образом устройстве нить диафрагмы наматывалась на вращающийся барабан, закрепленный на оси, к которой прикреплялось зеркальце, вращающееся вместе с барабаном. На зеркальце падал луч света; при поворотах зеркальца то в одну, то в другую сторону, происходивших в результате колебаний мембраны, луч отклонялся, и эти отклонения можно было записывать на светочувствительную бумагу. И только с развитием электроники были разработаны более или менее точные измерительные приборы, а для конструирования современного портативного шумомера пришлось дожидаться изобретения транзисторов.

По существу, современный шумомер — это электронный аналог старого механического устройства. Первым шагом в процессе измерения служит преобразование звукового давления в изменения электрического напряжения; это преобразование производит микрофон. В настоящее время в таких приборах применяют микрофоны самых различных типов: конденсаторные, с движущейся катушкой, кристаллические, ленточные, с нагретой проволокой, с сегнетовой солью — это лишь малая часть всех типов микрофонов. В нашей книге мы не будем рассматривать принципы их действия.

Все микрофоны выполняют одну и ту же основную функцию, и большинство из них снабжено мембраной, того или иного вида, которая приводится в колебания изменениями давления в звуковой волне. Смещения мембраны вызывают соответствующие изменения напряжения на зажимах микрофона. Следующий шаг в измерении — усиление, а затем выпрямление переменного тока и заключительная операция — подача сигнала на вольтметр, откалиброванный в децибелах. В большинстве таких приборов вольтметром измеряются не максимальные, а «среднеквадратичные значения» сигнала, то есть результат определенного вида усреднения, которым пользуются чаще, чем максимальными значениями.

Обычным вольтметром нельзя охватить огромный диапазон звуковых давлений и поэтому в той части устройства, где происходит усиление сигнала, имеется несколько цепей, различающихся по усилению на 10 дБ, которые можно включать последовательно одну за другой.

Однако до сих пор еще широко применяют усовершенствованную модель старого осциллографа. В электронно-лучевом осциллоскопе проблема инерционности, свойственная механическому осциллографу, полностью исключена, так как масса электронного луча пренебрежимо мала и он легко отклоняется электромагнитным полем и рисует на экране кривую колебаний напряжения, подаваемого на прибор.

Полученная осциллографическая запись применяется для математического анализа формы звуковой волны. Осциллоскопы также чрезвычайно полезны и при измерении импульсных шумов. Как мы уже говорили, обычный шумомер непрерывно определяет среднеквадратичные значения сигнала. Но, например, звуковой хлопок или орудийный выстрел не порождают непрерывный шум, а создают единичный, очень мощный, иногда опасный для слуха импульс давления, который сопровождается постепенно затухающими колебаниями давления (рис. 13). Начальный скачок давления может повредить слух или разбить оконное стекло, но так как он единичен и кратковременен, то среднеквадратичная величина не будет для него характерна и может только привести к недоразумению. Хотя для измерения импульсных звуков существуют специальные шумомеры, большая часть их не сможет зарегистрировать полностью среднеквадратичную величину импульса просто потому, что они не успевают сработать. Вот здесь осциллоскоп и демонстрирует свои преимущества, мгновенно вычерчивая точную кривую подъема давления, так что максимальное давление в импульсе можно измерить прямо на экране.

Рис. 13. Типичный импульсный шум.

Возможно, одним из наиболее существенных вопросов акустики является зависимость поведения звука от его частоты. Нижняя частотная граница восприятия звука человеком составляет около 30 Гц, а верхняя — не выше 18 кГц; поэтому шумомер должен был бы регистрировать звуки в том же диапазоне частот. Но тут возникает серьезное затруднение. Как мы увидим в следующей главе, чувствительность человеческого уха для различных частот далеко не одинакова; так, например, чтобы звуки с частотой 30 Гц и 1 кГц звучали одинаково громко, уровень звукового давления первого из них должен быть на 40 дБ выше, чем второго.

И следовательно, показания шумомера сами по себе еще не многого стоят.

Этой проблемой занялись специалисты по электронике, и современные шумомеры снабжены корректирующими контурами, состоящими из отдельных цепочек, подключая которые можно снизить чувствительность шумомера к низкочастотным и очень высокочастотным звукам и тем самым приблизить частотные характеристики прибора к свойствам человеческого уха. Обычно шумомер содержит три корректирующих контура, обозначаемых А, В и С; наиболее полезна коррекция А; коррекцию В применяют лишь изредка; коррекция С мало влияет на чувствительность в диапазоне 31,5 Гц — 8 кГц. В некоторых типах шумомеров используется еще коррекция D, которая позволяет считывать показания прибора прямо в единицах PN дБ, применяемых для измерения шума самолетов (см. Акуст. словарь). Точный расчет PN дБ весьма сложен, но для высоких уровней шума уровень в единицах PN дБ равен уровню в дБ, измеренному шумомером с коррекцией D, плюс 7 дБ; в большинстве случаев шум реактивных самолетов, выраженный в PN дБ, приблизительно равен уровню в дБ, измеренному шумомером с коррекцией А, плюс 13 дБ.

В настоящее время почти повсеместно уровень шума принимают равным уровню, измеренному в дБ при помощи шумомера с коррекцией А, и выражают его в единицах дБА. Хотя человеческое ухо воспринимает звук несравненно более утонченно, чем шумомер, и поэтому звуковые уровни, выраженные в дБА, ни в коей мере не соответствуют точно физиологической реакции, но простота этой единицы делает ее чрезвычайно удобной для практического применения.

Важнейший недостаток измерения громкости в дБА состоит в том, что при этом наша реакция на звуки низкой частоты недооценивается и совершенно не учитывается повышенная чувствительность уха к громкости чистых тонов.

К числу достоинств шкалы дБА следует, в частности, отнести то обстоятельство, что здесь, как мы увидим в следующей главе, удвоение громкости грубо соответствует увеличению уровня шума на 10 дБА.

Однако даже эта шкала дает не более чем грубое указание на роль частотного состава шума, а так как эта характеристика шума часто чрезвычайно важна, то результаты измерений, проведенных с помощью шумомера, приходится дополнять данными, полученными при использовании других приборов.

Частоты, как и интенсивности, измеряют в логарифмическом масштабе, причем за основу принимают ступени удвоения числа колебаний в секунду. Так как, однако, диапазон частот менее широк, чем диапазон интенсивностей, число десятикратных увеличений не подсчитывают, десятичными логарифмами не пользуются и частоты звука всегда выражают числом колебаний, или циклов в секунду. За единицу частоты принимают одно колебание в секунду, или 1 герц (Гц). Определение интенсивности звука для каждой частоты потребовало бы бесконечного числа измерений. Поэтому, как и в музыкальной практике, весь диапазон разделяют на- октавы. Самая большая частота в каждой октаве в два раза превышает самую малую. Первый, наиболее простой этап частотного анализа звука — измерение уровня звукового давления в пределах каждой из 8 или 11 октав, в зависимости от интересующего нас диапазона частот; при измерении сигнал с выхода шумомера поступает на набор октавных фильтров, или на октавный полосовой анализатор. Слово «полоса» указывает на тот или иной участок частотного спектра. Анализатор содержит 8 или И электронных фильтров. Эти устройства пропускают только те частотные компоненты сигнала, которые лежат в пределах их полосы. Включая фильтры по одному, можно последовательно измерить уровень звукового давления в каждой полосе непосредственно при помощи шумомера.

Но во многих случаях даже октавные анализаторы не дают достаточных сведений о сигнале, и тогда прибегают к более детальному анализу, применяя фильтры в половину или в одну треть октавы. Для получения еще более детального анализа используют узкополосные анализаторы, которые «разрезают» шум на полосы постоянной относительной ширины, например 6 % от средней частоты полосы или на полосы шириной в определенное число герц, например 10 или 6 Гц.

Если в шумовом спектре присутствуют чистые тоны, что случается нередко, их частоту и амплитуду можно установить точно с помощью анализатора дискретных частот.

Обычно звукоанализирующая аппаратура очень громоздка, и поэтому ее применение ограничивается рамками лабораторий. Весьма часто звук, подлежащий исследованию, через микрофон и усилительные цепи шумомера записывают на высококачественный портативный магнитофон, применяя для калибровки контрольные сигналы; затем запись проигрывают уже в лаборатории, подавая сигнал на анализатор, который автоматически вычерчивает частотный спектр на бумажной ленте. На рис. 14 изображены спектры типичного шума, полученные с помощью октавного, третьоктавного и узкополосного (полоса 6 Гц) анализаторов.

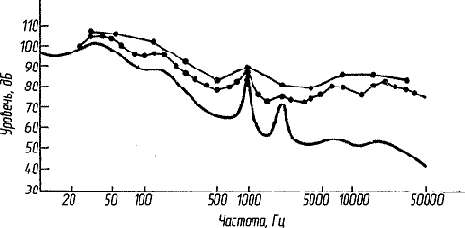Рис. 14. Анализ звука с помощью октавного и третьоктавного фильтров
и фильтра с шириной полосы 6 Гц.

Однако, чтобы измерить шум, еще недостаточно знать уровень громкости и частоту звука. Если говорить о шуме окружающей среды, то он складывается из множества отдельных шумов различного происхождения: это шумы уличного движения, самолетов, промышленные шумы, а также шумы, возникающие в результате других видов деятельности человека. Если попытаться измерить уровень шума на улице обычным шумомером, то окажется, что это чрезвычайно сложная задача: стрелка шумомера будет непрерывно колебаться в очень широких пределах. Что же следует принять за уровень шума? Максимальный отсчет? Нет, эта цифра слишком высока и непоказательна. Средний уровень? Это было бы возможно, но крайне трудно оценить среднюю величину для какого-то определенного промежутка времени, а чтобы удерживать стрелку в пределах шкалы, придется непрерывно менять ступени усиления шумомера.

Таблица 4
Статистическое распределение уровней шума при сильно флуктуирующем шумовом климате, показывающее время (в %), в течение которого был превышен каждый из уровней, указанных в первом столбце. (На основании этой таблицы путем интерполяции получены следующие значения: L1 = 94 дБА, L10 = 83 дБА, L50 = 72 дБА, L90 = 66 дБА и L99 = 60 дБА, с точностью до 1 дБ. )
Уровень шума, дБА	Время, в течение которого был превышен данный уровень, %
100	0
95	0,7
90	2,9
85	8,3
80	15
75	33,6
70	62,5
65	96,7
60	98,9
55	100

Существуют два общепринятых метода учета флуктуации уровня шума, позволяющие выражать этот уровень в численной мере. В первом методе используют так называемый анализатор статистического распределения. Это устройство регистрирует относительную долю времени, в течение которого измеряемый уровень шума находится в пределах каждой из ступеней шкалы, расположенных, например, через каждые 5 дБ. Результаты таких измерений показывают, в течение какой доли полного времени был превышен каждый из звуковых уровней. Нанеся на график числа, представленные в табл. 4, соединив точки плавной линией и установив уровни, которые были превышены в течение 1, 10, 50, 90 и 99 % времени, мы сможем дать удовлетворительное описание «шумового климата». Указанные уровни обозначаются так: L1, L10, L50, L90 и L99. L1 дает представление о максимальном значении уровня шума, L10 — это характерный высокий уровень, тогда как L90 как бы показывает шумовой фон, то есть уровень, до которого снижается шум при наступлении временного затишья. Большой интерес представляет разность между значениями L10 и L90; она указывает, в каких пределах в каждом данном месте варьируется уровень шума, а чем больше колебания шума, тем сильнее его раздражающее воздействие. Впрочем, уровень L10 и сам по себе служит хорошим показателем беспокоящего действия транспортного шума; этот показатель широко применяется при измерении и прогнозирования транспортного шума, и с его учетом определяют размеры государственной компенсации жертвам шума новых автострад и дорог (см. гл. 11). Итак, L10 — это уровень звука, выраженный в дБА, который превышается в течение точно десяти процентов от полного времени измерений.

Обычно транспортный шум флуктуирует вполне определенным образом, поэтому уровень L10 служит самостоятельным достаточно удовлетворительным показателем шума, хотя только частично представляет статистическую картину шума. Если же шумы меняются беспорядочно, как, например, это происходит при наложении друг на друга железнодорожных, промышленных и иногда самолетных шумов, распределение шумовых уровней сильно колеблется от точки к точке.

В подобных случаях также желательно выразить все статистические данные одним числом. Были сделаны попытки изобрести формулу, включающую всю картину шума, включая и размах шумовых флуктуации. К таким показателям относятся «индекс транспортного шума» и «уровень шумового загрязнения», но самый распространенный показатель — это особого рода средняя величина, обозначаемая Lэкв. Она характеризует среднее значение энергии звука (в отличие от арифметического усреднения уровней, выраженных в дБ); иногда Lэкв называют эквивалентным уровнем непрерывного шума, потому что численно эта величина соответствует уровню такого строго стабильного шума, при котором за весь период измерения микрофон принял бы то же суммарное количество энергии, какое поступает в него при всех неравномерностях, всплесках и выбросах измеряемого флуктуирующего шума. В простейшем случае Lэкв составит, например 90 дБА, если уровень шума все время равнялся 90 дБА, или если половину времени измерения шум составлял 93 дБА, а остальное время полностью отсутствовал. Действительно, так как удвоение интенсивности или энергии шума приводит к увеличению его уровня на 3 дБ, то для того, чтобы при удвоении интенсивности шума сохранить постоянным общее количество энергии, следует вдвое уменьшить время его действия. Аналогично ту же величину Lэкв = 90 дБА мы получим при уровне шума 100 дБА, если он действует в течение одной десятой того же промежутка времени. Измерение расхода электроэнергии при помощи электросчетчика производится подобным же образом. На практике периоды постоянного уровня шума и периоды полного его отсутствия встречаются не часто, и поэтому рассчитать Lэкв достаточно сложно. Здесь на помощь приходят таблицы распределения типа табл. 4, или специально сконструированные автоматические счетчики. Индекс Lэкв обладает двумя недостатками: при усреднении короткие всплески шума с высоким уровнем вносят больший вклад, чем периоды шума низкого уровня; кроме того, увеличение числа максимумов мало влияет на величину Lэкв.

Например, если при усреднении за день шума от 100 поездов получается эквивалентный уровень Lэкв = 65 дБА, то при увеличении числа поездов вдвое Lэкв возрастает всего на 3 дБА. Для того чтобы величина Lэкв возросла так же, как при удвоении громкости (то есть как при увеличении уровня на 10 дБА) шума, создаваемого каждым из поездов, их число пришлось бы увеличить в 10 раз. И все же, несмотря на некоторую неполноценность, шкала Lэкв представляет собой наилучшую универсальную меру шума из всех имеющихся в настоящее время. В Англии она постепенно получит такое же распространение, какое имеет на континенте. Сейчас она уже применяется в Англии для измерения дозы шума, получаемой лицами, работающими в промышленности по найму.

Применяется и другая мера, по существу гораздо более сходная с Lэкв, чем может показаться на первый взгляд: это нормировочный индекс шума, к сожалению слишком хорошо знакомый тем, кто живет вблизи крупных аэропортов. Шкалу нормировочных индексов шума используют для характеристики среднемаксимальных уровней шума самолетов, выраженных в PN дБ (так называемый «воспринимаемый уровень звука», см. Акуст. словарь), а так как она начинается от уровня 80 PN дБ (около 67 дБА), то значение 80 вычитается из величины среднемаксимального уровня. Теоретически, если за время измерения шум производит только один самолет, величина этого индекса будет точно равняться среднемаксимальному уровню в PN дБ минус 80. При каждом удвоении числа самолетов следует прибавлять к этому числу 4,5 единицы, а не 3, как для шкалы Lэкв. Хотя формула этого индекса и выглядит несколько ошеломляюще, выше нам удалось фактически полностью его охарактеризовать. Если отдельные пиковые уровни шума самолетов различаются всего на несколько дБ, усредненную величину можно вычислить арифметически. В противном случае значения уровня шума, выраженные в дБ, придется обратно переводить в величины интенсивности, и здесь потребуются таблица логарифмов и светлая голова!

Существует множество других мер, шкал и индексов для измерения шума, включая фоны, соны, нои, различные производные PN дБ и ряд других критериев, не считая всех международных вариантов шкалы нормировочных индексов шума. В главе 11 мы рассмотрим индекс, называемый «исправленный уровень шума», официально принятый в Англии для измерения промышленного шума. Заниматься описанием других единиц и показателей нет необходимости; следует отметить, что в США для измерения шума на рабочем месте принят показатель Lэкв, но при удвоении времени воздействия шума к его значению там прибавляют не 3 дБ, как в Европе, а 5 дБ. В остальном показатели дБА, L10 и Lэкв применяются одинаково во всем мире.

&nbsp

[11] Bell (бел) — по-английски значит колокол. — Прим ред.

Слух и повреждения слуха

Представьте себе устройство, с помощью которого одинаковой точностью можно взвесить и блоху, и слона! Это кажется невозможным, но ведь человеческое ухо выполняет не менее трудную задачу: самый громкий звук, воспринимаемый им, в 10 триллионов (1013) раз сильнее самого тихого; ухо анализирует звуки, различающиеся по частоте почти в 1000 раз. Мы довольно бойко заговорили об ушах и слухе. Однако что же такое слух? Что происходит на концах этих трубочек? На первый взгляд все кажется совершенно ясным: уши — это орган восприятия звуков. Но устройство их столь тонко и сложно и действуют они сообща с такой точностью, достойной вычислительной машины, что до сих пор наука еще не до конца проникла в их тайну.

Что делают уши? Они воспринимают звук и разлагают его на компоненты, действуя одновременно и как узкополосные анализаторы, и как анализаторы дискретных частот. Они передают в мозг кодированную информацию, достаточно богатую подробностями, что позволяет интерпретировать или идентифицировать звуки и понимать сложную речь. Уши осуществляют также обратную связь, позволяя человеку управлять своей речью; с их помощью мы определяем направление и расстояние до источника звука; из громкого неупорядоченного шума уши могут выделить регулярные звуки, что делает возможным разбирать речь, заглушаемую шумом. В ушах находятся также и органы равновесия. Словом, несмотря на кажущуюся простоту, уши относятся к самым сложным органам человеческого тела, хотя мы и привыкли воспринимать их существование и действие как нечто обычное.

В ухе различают три самостоятельные отдела: наружное, среднее и внутреннее ухо (рис. 15). Лучший способ разобраться в строении уха — это проследить путь, который проходит звуковая волна, прежде чем мы услышим звук. Из гл. 3 мы уже знаем, что, когда звуковая волна бежит по трубе и достигает ее открытого конца, внезапное столкновение волны с бесконечно большим объемом наружного воздуха вызывает почти полное ее отражение.

И наоборот, когда звук бежит в воздухе и встречает на своем пути открытый конец трубы, он входит в трубу, обладая лишь малой долей интенсивности наружной волны.

Рис. 15. Ухо.

Часть уха, которую в просторечии мы называем ушным отверстием, — в науке она именуется наружным слуховым проходом — представляет собою трубку. Сама по себе эта трубка не могла бы достаточно эффективно воспринимать звуки из внешнего мира ввиду, говоря техническим языком, несогласования импедансов слухового прохода и внешней среды; без близкого согласования импедансов здесь, как и в радиотехнике, невозможна достаточно полная передача энергии. Это затруднение преодолевается с помощью мясистой лепешки с хрящами, называемой ушной раковиной, которую по незнанию часто недооценивают, не признавая за ней акустической функции. Ушная раковина благодаря особенностям своей формы делает более плавным переход от наружного воздуха к воздуху в слуховом проходе, что несколько увеличивает долю звуковой энергии наружной волны, попадающей в слуховой проход. Ушная раковина аналогична антенне в радиотехнических устройствах.

Проникнув в наружный слуховой проход, звук распространяется далее как плоская волна и через 2— 3 см встречает на своем пути барабанную перепонку. Она представляет собой мембрану, которая удерживается в состоянии известного натяжения двумя мышцами, tensor tympani и tensor stapedius, и приводится в движение в результате колебания давления в наружном слуховом проходе. К барабанной перепонке присоединены три малые косточки: молоточек, наковальня и стремя, которые находятся в заполненной воздухом костной полости. Форма стремени оправдывает его название; своим основанием стремя упирается в овальное окно — отверстие, ведущее во внутреннее ухо. Среднее ухо с его тремя косточками — еще одно приспособление для согласования импедансов; его можно считать акустическим трансформатором.

Три косточки, объединенные названием «слуховые косточки», образуют плечи рычага, длины которых относятся приблизительно как 3:1, и если учесть, что поверхность овального окна во много раз меньше поверхности барабанной перепонки, то оказывается, что давление, передаваемое на овальное окно, приблизительно в 20 раз больше, чем давление, испытываемое барабанной перепонкой.

Среднее ухо соединено с носоглоткой евстахиевой трубой, получившей свое название по имени открывшего ее итальянского анатома. При глотании евстахиева труба открывается и давление по обе стороны барабанной перепонки выравнивается, что существенно, в частности, для компенсации изменений давления, которые происходят, например, при подъеме на высоту. Вероятно, каждому, кто летал на самолетах, внутри которых давление не поддерживается достаточно постоянным, приходилось испытывать ослабление слуха или боль в ушах при посадке или на взлете; эти ощущения особенно сильны при насморке. Причина их — падение или увеличение атмосферного давления снаружи барабанной перепонки, когда давление внутри среднего уха сохраняется неизменным. В этих условиях барабанная перепонка оказывается под действием одностороннего давления, что снижает ее способность к колебаниям и вызывает некоторую тугоухость. При достаточно сильном давлении на барабанную перепонку появляется боль в ушах.

Обычно при глотании все эти ощущения исчезают; евстахиева труба открывается, воздух проходит в полость среднего уха или выходит из нее, и давление по обе стороны барабанной перепонки уравнивается. Затем евстахиева труба вновь закрывается, и барабанная перепонка может возобновить колебания. Но при насморке евстахиева труба и даже полость среднего уха наполнены слизистыми выделениями, и выравнивание давления может не произойти. В среднем ухе часто содержится небольшое количество жидкости, которая выводится при глотании, но если полость заполнена слизью, то колебания слуховых косточек тормозятся вязкостью жидкости, и это еще более снижает чувствительность слуха.

Слуховой процесс завершается после того, как колебания косточек передаются во внутреннее ухо. Этот отдел представляет собой сложную систему трубочек, заключенных в кость черепа, и называется лабиринтом. В нем объединены два различных органа; одна его часть — это вестибулярный аппарат, включающий полукружные каналы и не имеющий отношения к слуховому процессу. Вестибулярный аппарат — это устройство для измерения углового ускорения тела, позволяющее удерживать равновесие. Другая часть лабиринта, улитка, — самый сложный элемент уха. С виду она похожа на очень маленькую раковину улитки и состоит из спиральной трубочки, заполненной жидкостью, называемой перилимфой; улитка делится перегородкой на две параллельные полости: верхний и нижний каналы. Эти каналы на конце улитки соединяются небольшим отверстием в перегородке, называемым геликотремой.

Если бы спиральную трубочку улитки удалось развернуть, она приобрела бы форму, изображенную на рис. 16, а. Движение стремени в овальном окне вызывает колебания перилимфы, возможные благодаря тому, что круглое окно, расположенное в конце нижнего канала, затянуто гибкой мембраной, которая допускает, перемещение практически несжимаемой жидкости.

Рис. 16. Схема «развернутой» улитки (а). Сечение витка улитки (б).

Перегородка улитки состоит из мембраны Рейсснера и базилярной мембраны и содержит другую жидкость — эндолимфу. В пространстве между этими двумя мембранами находится орган Корти, содержащий приблизительно 24 000 так называемых волосковых клеток, расположенных на базилярной мембране, имеющей волокнистую структуру, напоминающую струны арфы. Специалисты пока еще не пришли к единодушному мнению относительно того, как именно эти клетки, связанные с нервными окончаниями и слуховым нервом, реагируют на колебания перилимфы. Некоторые ученые считали ранее, что волокна базилярной мембраны находятся в состоянии натяжения и их резонансная частота (вспомним натянутую струну) прогрессивно понижается с удалением от основания мембраны овального окна, а частотный анализ звука осуществляется благодаря тому, что каждое волокно возбуждается только на своей собственной частоте.

Сейчас наибольшим признанием пользуется теория Георга фон Бекеши. Согласно этой теории, волокна не натянуты и сложные механические силы вызывают изгибание базилярной мембраны в разных точках (в зависимости от частоты звука) по ее длине; при этом орган Корти испытывает сдвиговые напряжения в соответствующих точках, что в свою очередь вызывает возбуждение нервных волокон.

Однако довольно физиологии. Поговорим лучше о том, что именно слышат уши, потому что для жертв шума это гораздо важнее, чем как именно они слышат. Самый низкий тон, воспринимаемый человеком с нормальным слухом, имеет частоту около 20 Гц. Точно установить нижнюю границу шкалы слышимости довольно трудно, поскольку звуки с частотой ниже 20 Гц нередко воспринимаются не органом слуха, а другими участками нервной системы. Верхний предел слухового восприятия сильно различается у разных людей. Особое значение здесь имеет возраст. В восемнадцать лет при безупречном слухе можно услышать звук до 20 000 Гц [20 кГц (килогерц)], но в среднем границы слышимости для любого возраста лежат в интервале 18—16 кГц. Некоторые люди почти постоянно ощущают в ушах слабый звон очень высокой частоты, что мешает им различать внешние раздражители подобной частоты.

Термины «высота звука» и «частота звука» отнюдь не равнозначны. Частота — это физическая величина, характеризующая звуковую волну, а высота тона — чисто субъективное ощущение, которое зависит не только от частоты. При больших интенсивностях высота звука повышается как на высокой, так и на низкой частоте, при малой же интенсивности низкочастотного звука его частота может изменяться примерно на 5 % без заметного для слушателя изменения высоты.

Высота тона и частота не являются синонимами еще и по той причине, что сложные звуки часто обладают определенной высотой, но в действительности состоят из целого ряда частот. Так, например, звук скрипки имеет определенную высоту, но содержит множество гармоник, имеющих различные частоты.

Высота, которую обычно приписывают такому звуку,— это высота основной частоты, или первой гармоники; однако, как оказывается, если из такого сложного звука убрать основную частоту, его высота останется для слушателя той же, изменится только окраска тона, или тембр. Это следует считать слуховой иллюзией: показано, что в подобных случаях отсутствует возбуждение в том участке улитки, который обычно возбуждается на основной частоте.

С возрастом чувствительность человеческого уха к высокочастотным звукам постепенно падает; это совершенно нормальный процесс, называемый пресбикузисом. На рис. 17 показано обычное течение этого процесса. Кривые, соответствующие самым низким слышимым уровням звука для различных частот, одновременно отражают одно из важнейших явлений акустики: слух гораздо чувствительнее к звукам в области 4 кГц, чем к более низким или более высоким звукам. Обычно звук частотой 30 Гц слышен только при уровне звукового давления 60 дБ, тогда как для молодого человека с хорошим слухом порог слышимости на частоте 4 кГц может опускаться, как известно, до ?2 дБ. Знак «минус» не должен никого смущать: он вовсе не означает, что речь идет о количествах звука, «меньших, чем отсутствие звука». Вспомним, что уровень звукового давления обычно выражают в децибелах относительно уровня 0,00002 Н/м2. Если измеряемое звуковое давление меньше этой величины, уровень в дБ выражается отрицательным числом. Впрочем, практически уровень окружающего шума никогда не бывает настолько низок, чтобы удалось расслышать звук уровня ?2 дБ. Указанное выше различие в чувствительности слуха, как показано на рис. 17, становится гораздо менее заметным при возрастании звукового уровня, а когда звуковой уровень значительно превышает 130 дБ, то независимо от частоты звук вызывает болевое ощущение. Звуки с уровнем порядка 150 дБ при любой частоте немедленно приводят к повреждению слуха.

Вопросом повреждения слуха под воздействием шума мы займемся немного позже, а сейчас, пока мы еще не забыли физиологию уха, интересно ознакомиться с двумя защитными приспособлениями, созданными самой природой, которые в какой-то мере предохраняют ухо от повреждения шумом.

Одно из них известно под названием ушного рефлекса. Мышца tensor tympani удерживает барабанную перепонку в состоянии легкого натяжения; эта мышца состоит из двух небольших мышц, которые тянут барабанную перепонку внутрь, а стремя — наружу. Если ухо подвергается воздействию шума, превышающего приблизительно 90 дБ, в течение времени свыше 10 мс (миллисекунд), происходит рефлекторное сокращение мышцы tensor tympani, в результате все механические части среднего уха становятся более жесткими, что снижает чувствительность к звукам низкой и средней частоты. Встречаются счастливчики, обладающие способностью произвольно управлять ушным рефлексом: зная о предстоящем громком звуке, они могут сократить мышцу и тем самым защитить свой слух.

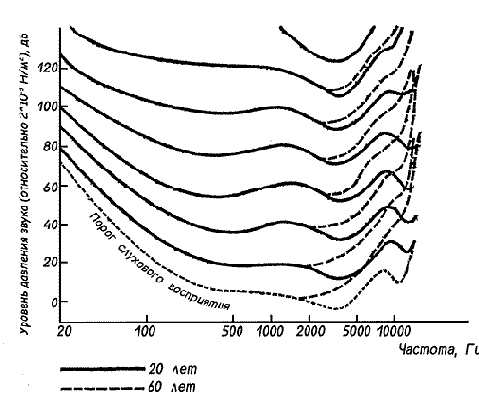Рис. 17. Линии равной громкости для чистых тонов (для людей различных возрастов).

Второе защитное приспособление состоит в изменении характера колебаний ушных косточек. В условиях нормальной функции при шуме обычной интенсивности под воздействием колебаний слуховых косточек стремя приобретает поступательное движение, которое через основание стремени и овальное окно передается перилимфе, заполняющей верхний канал улитки. Но если кто-то, к своему несчастью, окажется с незащищенными ушами под воздействием шума свыше 140 дБ, то характер колебаний молоточка, наковальни и стремени у него резко изменится — они начнут качаться из стороны в сторону. При таком движении основания стремени перилимфа не будет двигаться вдоль улитки, а станет только перемещаться с одной стороны овального окна к другой. При этом колебания давления в перилимфе заметно уменьшатся; поэтому, как только косточки начнут колебаться подобным образом, громкость воспринимаемого звука мгновенно упадет.

Как видно из рис. 17, ухо не только значительно менее чувствительно к звукам низкой частоты, но, кроме того, неравномерно оценивает громкость на различных частотах. Можно было бы предположить, что при удвоении уровня звукового давления удваивается и громкость, однако это не так.

В предыдущей главе мы говорили, что удвоение звукового давления соответствует увеличению уровня звука на 6 дБ. Если однако, мы измерим в децибелах уровень какого-нибудь звука, а потом будем усиливать его до тех пор, пока он не покажется нам вдвое громче, то обнаружим, что уровень звукового давления увеличится приблизительно на 10 дБ; иными словами, звуковое давление возросло более чем в три раза. Из гл. 2 мы знаем, что это соответствует усилению интенсивности звука (плотности потока энергии на единицу поверхности) в 10 раз.

Как звуковой анализатор ухо обладает одним очень существенным недостатком: в присутствии чистого тона определенной частоты ухо не воспринимает звуки близких частот и меньшей интенсивности (рис. 18). Это явление, называемое маскировкой, имеет место не только при чистых тонах, но и при любых звуках. Впрочем, иногда маскировка чрезвычайно удобна: например, в тех случаях, когда желательно, чтобы какой-то разговор не был слышен посторонним, часто значительно проще ввести дополнительный звук, чем понизить звуковой уровень речи.

Рис. 18. Маскирующее действие чистого тона.

А как обстоит дело с другими свойствами нашего слуха: определением направления и расстояния, различением отдельных дискретных составляющих на фоне сплошного шумового спектра, а не только простого восприятия высоты отдельной заданной ноты? Оба эти свойства нашего слуха обусловлены наличием двух ушей; у людей, страдающих понижением слуха в одном ухе, эти способности отсутствуют. Как определяется направление прихода звука, понятно из рис. 19. Если только источник звука расположен не в плоскости симметрии головы, расстояния от источника звука до каждого из ушей различны и, следовательно, до одного уха звук дойдет на какую-то малую долю секунды раньше, чем до другого. Мозг в состоянии измерить» эту разницу во времени и таким образом определить направление, откуда идет звук. Однако точность такого определения не очень высока, поскольку, если расстояние до источника звука неизвестно, угол, под которым приходит звук, нельзя определить, зная только разницу во времени прихода звука.

Впрочем, на основании опыта слушатель часто может определить расстояние до источника звука, исходя из его громкости, а в случае удаленных источников — учитывая частотный спектр звука, который претерпевает известные изменения в результате поглощения в атмосфере и влияния окружающей среды, что приводит к затуханию высокочастотных звуков. Кроме того, за исключением случая, когда источник расположен почти в плоскости симметрии головы, одно ухо всегда находится в звуковой тени, так сказать, «за углом», и звук доходит до него только в результате дифракции на лицевой или затылочной части головы. Это обстоятельство усиливает разницу во времени между импульсами, поступающими в мозг от обоих ушей, а также снижает громкость звука, попадающего в затененное ухо.

Рис. 19. Определение направления прихода звука.

Из сказанного легко понять, что установить местоположение источника низкочастотных звуков гораздо труднее, чем высокочастотных, так как в первом случае разница во времени сказывается много меньше, чем во втором. Кроме того, как мы узнаем в гл. 6, низкочастотный звук в гораздо большей степени огибает препятствия в результате дифракции, чем высокочастотный, вследствие чего разница в громкости звуков, воспринимаемой каждым ухом, еще более снижается.

Еще одно преимущество бинаурального слуха (с помощью обоих ушей) связано с основным различием между звуком, состоящим из чистых тонов, и случайным звуком, подобным в известном смысле хаотическому движению молекул воздуха. Если нужно уловить гармонический звук, например, сквозь шум ветра, человеческое ухо справляется с этой задачей много лучше любого электронного инструмента, за исключением вычислительной машины. Причина этого проста, и соответствующий процесс совершенно аналогичен корреляционному методу анализа звука с помощью вычислительной машины.

У взрослого человека расстояние между ушами составляет 150—200 мм, что, как мы уже говорили, почти всегда приводит к заметной разности фаз между звуками, приходящими к каждому из ушей.

Произведение таких двух сигналов для периодического и для случайного исходного звука зависит от сдвига фаз по-разному: для периодического звука среднее значение произведения зависит от разности фаз также периодически; для случайного же звука среднее значение произведения быстро падает при увеличении разности фаз. Это обстоятельство и позволяет различать периодический или гармонический звук на фоне случайного шума. Последние абзацы, по-видимому, особенно интересны для любителей высококачественного воспроизведения звука с помощью стереофонических устройств, которые, однако, были созданы в первую очередь для того, чтобы придать воспроизводимому звуку дополнительное «измерение», что позволяет создать эффект бинаурального (или стереофонического) восприятия звука.

Не слишком отклоняясь от темы настоящей главы, рассмотрим еще одно явление, связанное с бинауральным восприятием звука, а именно чревовещание. По своей сути чревовещание значительно более сложная иллюзия, чем кажется. Как мы уже видели, наша способность определять направление звука при слушании обоими ушами имеет слабое звено (его можно ликвидировать, используя третье электронное «ухо»— микрофон): разность по времени или по фазе в восприятии звука каждым ухом указывает направление только в том случае, если известно расстояние до источника звука, но и тогда зачастую не слишком точно. Когда кто-нибудь говорит с нами, всегда более или менее очевидно, откуда именно идет звук, потому что мы видим, как человек шевелит губами и двигает челюстью. В подобных случаях мозг срабатывает безошибочно, и его невозможно убедить, что звук идет из какого-либо другого места. Но если человек сжал челюсти и говорит без каких-либо видимых признаков речи, зрительно определить расстояние до источника звука уже невозможно и процесс отыскания направления становится менее четким. Если чревовещатель достаточно ловок для того, чтобы теми или иными неакустическими средствами заставить слушателя сосредоточить внимание на каком-то не слишком удаленном предмете, мозг учтет визуальное расстояние до этого предмета при «вычислении» фазовой разности между ушами; в результате у слушателя возникает подлинное ощущение, что звук приходит именно от этого предмета.

Если в качестве последнего выбрана какая- нибудь весьма эффектная подвижная кукла, то впечатление бывает достаточно сильным. Впрочем, теперь чревовещатели обычно появляются только на экранах телевизоров; здесь акустический эффект чревовещания совершенно теряется, и зритель видит лишь какое-то кукольное представление и человека, говорящего с закрытым ртом.

Конечно, уши не всегда работают так идеально, как следовало бы. Несчастный случай болезнь, воздействие шума — все это может серьезно нарушить их функцию. Инородное тело может прорвать барабанную перепонку, а удар по голове вызвать повреждение среднего или внутреннего уха. Болезнь может поразить среднее ухо или уничтожить чувствительные волосковые клетки на базилярной мембране, но хуже всего, когда произойдет повреждение слухового нерва и нарушатся его связи с головным мозгом — тогда бедняга, с которым это случилось, становится «глухим как пень», наступает глухота восприятия.

При всех видах глухоты, кроме последнего, медицина в состоянии помочь пострадавшему: поврежденные барабанную перепонку и слуховые косточки заменяют путем трансплантации или вживления искусственных косточек из пластмассы. Если волосковые клетки в улитке начинают терять чувствительность — может помочь усиление звука, поступающего в наружный слуховой канал; но когда погибает слуховой нерв — ухо как орган чувств становится совершенно бесполезным. Я надеюсь, что когда-нибудь станет возможным такое возбуждение других участков нервной системы; которое приведет к «искусственному» слуху. Ощущение боли чем-то сходно со слухом. Боль часто имеет «тональную характеристику»: у булавочного укола — высокий тон, у головной боли — низкий. Возможно, уже не за горами то время, когда путем возбуждения соответствующих участков нервной системы несчастным людям с погибшим слуховым нервом вновь будет дана возможность воспринимать звук. Слепому, безусловно, можно дать простейший вид «зрения», используя его спину как своего рода телевизионный экран, и действуя на различные участки спины с определенными силами в соответствии с находящимися перед ним предметами.

В настоящее время исследуется также возможность введения сигналов непосредственно в мозг.

Ухо может быть повреждено в результате болезни, но гораздо тревожнее тот факт, что только у малого числа взрослых мужчин слух не поврежден шумом; поэтому, в частности, почти невозможно установить, какой слух следует считать «нормальным» для мужчин. Чем это вызвано? Здесь можно назвать несколько причин. Мало кто из мужчин, достигших среднего возраста, ни разу в жизни не пользовался огнестрельным оружием, причем с незащищенными ушами; многие участвовали в военных действиях. Хотя в настоящее время во всех видах войск ясно отдают себе отчет в том, какую опасность представляет шум, и даже вносят своими работами немалый вклад в изучение этого вопроса, многие любители стрелкового спорта и охотники забывают, что каждый выстрел — это еще один шаг к тугоухости. В военных школах мальчики подвергаются действию шума ружейных выстрелов, что представляет серьезную опасность для слуха, особенно на закрытых стрельбищах; 12-калиберные охотничьи ружья приносят не меньше вреда, чем боевые винтовки. Ушные протекторы, о которых пойдет речь в гл. 14, обязательны для всех, кто пользуется любым огнестрельным оружием. Однако при этом необходимо соблюдать величайшую осторожность, поскольку такая защита ушей может привести к несчастному случаю, если помешает человеку услышать предостерегающий окрик.

Самая распространенная и серьезная причина тугоухости, вызванной шумом, — это воздействие высоких уровней шума на рабочих местах, будь то кабина дизельного грузовика, литейный завод или другие самые различные предприятия — от типографии до фабрики синтетических материалов. Если исключить взрывы и стрельбу, то повреждение слуха шумом вне связи с работой — событие маловероятное. Как бы ни раздражал человека шум самолетов или наземного транспорта, он вряд ли может вызвать физиологическое повреждение слуха. Возможно, исключение составляют мотоциклы некоторых марок и, как мы уже говорили, оркестры поп-музыки.

Как же именно воздействует шум на свои жертвы? Какой уровень шума следует считать опасным? Обратимы ли повреждения слуха?

Шум может повлиять на слух трояким образом: вызвать мгновенную глухоту или повреждение органа слуха; при длительном воздействии — резко снизить чувствительность к звукам определенных частот, и, наконец, шум может снизить чувствительность слуха на ограниченное время — минуты, недели, месяцы, после чего слух восстанавливается почти полностью.

Первый тип поражений — акустическая травма — обычно вызывается воздействием шума очень большой интенсивности, например взрыва. По очевидным причинам установить экспериментально минимальный уровень шума, приводящего к повреждениям такого рода, невозможно; но, по-видимому, импульсный шум, превышающий 150 дБ, вызывает травму мгновенно. При этом барабанная перепонка может оказаться непоправимо разорванной, а слуховые косточки сломанными или смещенными. Однако не исключено, что улитка все-таки уцелеет, поскольку повреждение косточек может помешать передаче всей энергии шума в перилимфу.

Говоря об импульсном шуме, следует отметить одно существенное обстоятельство, связанное со сказанным в предыдущей главе. Большая часть шумомеров определяет не максимальное значение давления в звуковой волне, а среднеквадратичное, то есть некоторую усредненную величину. Это удобно для измерения непрерывного шума и дает результаты хорошо совпадающие с субъективной слуховой оценкой шума; однако при измерении импульсного шума, когда нередко наблюдается всего один максимум с очень крутыми подъемом и падением, среднеквадратичная величина дает безнадежно заниженную оценку уровня шумового импульса. К тому же быстродействие обычных шумомеров, как правило, недостаточно для того, чтобы стрелка успела дойти хотя бы до среднеквадратичной величины. Для измерения импульсного шума лучше всего либо получить изображение звуковой волны на электронно-лучевом осциллографе и измерить максимальный уровень по делениям на экране, либо воспользоваться специальным импульсным шумомером.

Взрывы не единственный источник импульсного шума. Удар молотом, по стальной пластине также производит значительный импульс шума, хотя и не столь высокого уровня, как взрыв. Импульсы меньших интенсивностей тоже травмируют слух, но вызывают повреждения не в среднем, а во внутреннем ухе, как и непрерывный шум, о котором речь еще впереди. Что касается импульсного шума, то здесь человек в своей эволюции явно отстал от развития техники. Как мы уже знаем, в человеческом ухе есть два защитных устройства: одно из них — ушной рефлекс. К несчастью, он срабатывает в течение примерно 10 мс (миллисекунд), а за это время импульсный шум уже может вызвать травму. Но подобный импульсный шум с очень коротким временем нарастания почти никогда не встречается в природе, он порождается только человеком. Следовательно, природа вовсе не «зазевалась», допустив задержку ушного рефлекса, а просто «не приняла в расчет» обстоятельств, не существовавших в течение миллионов лет. Следующим шагом эволюционного процесса в этом направлении, несомненно, будет развитие способности к произвольной активации рефлекса при первых же признаках угрожающе громкого шума у значительно большего числа людей, чем число «счастливчиков», обладающих этой способностью уже сегодня. Как мне кажется, можно научиться произвольно вызывать у себя ушной рефлекс. Иногда нетрудно уловить момент, когда этот рефлекс вступает в действие — при этом часто слышно слабое щелкание, без сомнения связанное со смещением ушной серы около барабанной перепонки при натяжении последней. За этим щелчком следует понижение чувствительности слуха.

Еще один мощный источник импульсного шума — это звуковой хлопок, создаваемый самолетом. Прежде всего следует сказать, однако, что, по общепринятому мнению, для разрыва барабанной перепонки требуется пиковое избыточное давление в 35 000 Н/м2, а для повреждения легких — 100 000 Н/м2. Избыточное же давление, создаваемое сверхзвуковыми самолетами, очень редко превышает 100 Н/м2.

Избыточное давление свыше 6000 Н/м2 люди переносят без каких- либо вредных физиологических последствий, так что здесь мы еще имеем достаточный запас «прочности». Однако психологическая реакция становится значительной, и люди начинают выражать свое неудовольствие вслух уже приблизительно при 50 Н/м2; при избыточном давлении в 50—100 Н/м2 изредка возникают мелкие повреждения зданий, но общественное возмущение становится громогласным.

Может показаться странным, почему этот тип шума не выражают в децибелах, как все прочие шумы. Разумеется, сделать это вполне возможно. Тогда приведенные цифры преобразятся следующим образом: 185 дБ — разрыв барабанной перепонки, 194 дБ — повреждение легких, 134 дБ — оглушительное и 128 дБ — умеренное негодование общества (все эти цифры взяты относительно уровня 2×10?5 Н/м2). Однако звуковой хлопок настолько сильно отличается от обычного шума и наступает так внезапно, что данные, выраженные в децибелах, только создают неясность. Кроме того, если требуется установить степень воздействия шума на людей и здания, необходимо знать действительную величину максимального давления, с которым действует звуковая волна. О причинах звукового хлопка мы поговорим в гл. 6.

Однако повреждение слуха импульсным шумом — это еще не главная причина для беспокойства. Гораздо более пагубны для слуха длительные периоды непрерывного воздействия шума большой интенсивности. Этот вид шума действует двояко, причем первый вид воздействия может и не причинить серьезного вреда. Так, если человек подвергается долее чем несколько минут воздействию звука средней или высокой частоты с уровнем около 90 дБ или немного выше, он испытывает после этого так называемый «временный сдвиг порога». Нормальный порог слухового восприятия — это самый низкий уровень, при котором данный человек еще слышит звук той или иной частоты; после воздействия сильного шума этот порог заметно повышается.

Допустим, человек в нормальных условиях слышит звук частоты 4000 Гц при уровне звукового давления в 5 дБ. Уровень фонового шума обычно много выше 5 дБ, и поэтому измерения порогов слухового восприятия следует производить в специально оборудованных помещениях с очень низким уровнем окружающего шума, подавая звуковые сигналы через головные телефоны. Эта методика называется аудиометрией; она позволяет получить кривую индивидуальной чувствительности слуха, или аудиограмму. Обычно на аудиограммах отмечают отклонения от нормальной чувствительности слуха, а не действительный порог слышимости.

Рис. 20. Аудиограмма типичного сдвига порога слышимости после кратковременного воздействия шума.

Подвергнем испытуемого в течение 10 мин воздействию шума в частотной полосе 1200—2400 Гц при уровне звукового давления, скажем, 100 дБ; немедленно после прекращения шума у него обнаружится понижение чувствительности слуха. Если раньше он слышал звук в 4000 Гц при уровне в 5 дБ, то, чтобы он смог его услышать после шумового воздействия, звук придется усилить до 20 дБ. Однако такое понижение слуха продолжится не более получаса, после чего остаточный сдвиг порога станет незаметным. На рис. 20 представлена типичная аудиограмма, снятая немедленно после такого шумового воздействия. На ней можно заметить некоторое несоответствие частот: сдвиг порога сильнее всего выражен для частоты 4000 Гц, хотя шум, вызвавший сдвиг, звуков этой частоты не содержал. Такое несоответствие характерно для понижения слуха, вызванного шумом, и причины его пока не вполне ясны. Почти всегда наибольший сдвиг порога слышимости наблюдается на более высокой частоте, чем частота шума, вызвавшего сдвиг.

С увеличением времени воздействия и при повышении уровня шума увеличивается временный сдвиг порога и удлиняется период восстановления. Если, например, шум в 100 дБ при частотах 1200—2400 Гц длился 100 мин, то временный сдвиг порога превзойдет 30 дБ, а для восстановления нормального слуха потребуется около 36 ч.

Если воздействие сильного шума не происходит систематически, то остаточный эффект столь незначителен, что им можно пренебречь. Однако множество людей во всем мире постоянно подвергаются на производстве или других работах воздействию высоких уровней шума; эффект перестает быть временным, и с годами понижение слуха становится тяжелым и хроническим. Обычно жертвы шума склонны отрицать, что у них не все благополучно со слухом. Мне приходилось бывать на многих шумных заводах, где говорили: «Да, действительно, уровень шума у нас высокий, но мы привыкли и наша «терпимость» к шуму возросла». Чепуха! Происходит вот что: человек приходит на работу, где уровень шума высок, и, конечно, у него нет привычки к шуму. В конце первого рабочего дня у него возникнет сильный временный сдвиг порога, который, возможно, будет сопровождаться звоном в ушах («тинитус»). Если он поедет домой на своей машине, то обнаружит, что ее мотор стал шуметь как двигатель машины более высокого класса, ибо он не услышит дребезжания и скрипа, в особенности шумов, близких по частоте к 4000 Гц. Дома голос жены будет звучать так же громко, как обычно, но у него возникнет ощущение, что она говорит как бы через одеяло. Если у него нет других нарушений слуха, то он заметит, что звучание высокочастотных звуков неестественно усилилось; это обусловлено тем, что сравнительно со значительной потерей чувствительности к частотам около 4000 Гц потеря ее на более высоких частотах ничтожна. Шум окажет действие и на психику — человек почувствует сильную усталость.

На следующее утро слух у него частично восстановится, звон в ушах прекратится, а усталость пройдет после сна. Второй и последующие дни работы повлияют на него гораздо меньше. У него уже установится сдвиг порога слышимости, и поэтому шум покажется ему не таким громким. Он привыкнет к некоторому понижению слуха и, возможно, перестанет испытывать звон в ушах. Если спустя некоторое время, вплоть до одного года, — это зависит от характера и уровня шума, — этот человек оставит шумную работу и перейдет на тихую, через несколько недель, а возможно, месяцев его слух восстановится в удовлетворительной степени.

Однако, если он не изменит работы, наступит момент, когда восстановление слуха будет уже невозможно, и в конце концов он сам начнет замечать, что острота слуха у него понизилась и ему стало труднее разбирать слова. Он обнаружит, что понимает, что говорится по телевизору, только тогда, когда звук очень громкий, даже по его собственному ощущению.

На этой стадии повреждение стало стойким и необратимым. С годами провал в области 4000 Гц на аудиограмме этого человека все более углубляется, а затем и расширяется — чувствительность слуха снижается и на других частотах. К старости он станет совсем тугоухим (рис. 21).

Рис. 21. Типичные аудиограммы, показывающие потерю слуха у ткачей.

Итак, мы обсудили симптомы. А что можно сказать о причинах? Какой силы и какого рода шум причиняет повреждения? Проводились обширные исследования, и в 1972 г. Министерством труда был выпущен Кодекс правил по уменьшению дозы шума, получаемой работающими по найму, разработанный на основе наблюдений случаев повреждения слуха у лиц, занятых в промышленности. Эти исследования выполнены проф. Бэрнсом из Медицинского института (Чаринг-Кросс) и доктором Робинсоном из Национальной физической лаборатории. Пределы допустимого шума, указанные в кодексе, были установлены с оглядкой на реальность соблюдения их предпринимателями; некоторые эксперты считают эти пределы завышенными на 5 дБ. А если бы было возможно вообще пренебречь практическими трудностями, эти пределы следовало бы понизить на 10 дБ.

В предыдущей главе мы говорили об эквивалентном уровне непрерывного шума, обозначаемом Lэкв. Эта шкала особенно удобна в тех случаях, когда необходимо установить критерий риска повреждения слуха, поскольку она дает готовый рецепт для учета очень различных уровней шума, с которыми сталкивается разнорабочий, который в течение коротких периодов времени находится на разных участках завода с разными уровнями шума. В простейшем случае, когда рабочий проводит вблизи одной и той же машины 8 ч в день, предельный уровень шума, допускаемый кодексом, равен 90 дБА; так как в этом случае шум все время постоянен, то и по шкале Lэкв этот предел равен 90 дБА.

Если работающий подвергается воздействию шума всего четыре часа в день, а остальное время работает в условиях тишины, предельный уровень шума, установленный кодексом, равен 93 дБА, потому что при сокращении вдвое времени воздействия шума суммарная величина Lэкв сохраняется, если увеличить вдвое энергию шума (то есть повысить уровень на 3 дБ). В кодексе приведен также метод вычисления Lэкв для случая суммарного воздействия различных уровней шума в течение разных промежутков времени, но самый простой, хотя и более дорогой способ учитывать все вариации уровней шума со временем — это измерение Lэкв при помощи шумомеров специальной конструкции. Некоторые из них включают небольшие съемные элементы, так называемые дозиметры, которые обследуемый носит на себе; время от времени их показания снимаются с помощью основного устройства, и таким образом определяется доза шума. В табл. 5 приведены предельно допустимые дозы воздействия различных постоянных уровней шума в виде максимального времени, в течение которого можно ежедневно находиться под воздействием этого шума без риска повреждения слуха.

Таблица 5
Критерий риска повреждения слуха, полная ежедневная доза воздействия
Продолжительность воздействия	Предельно допустимые дозы, дБА
8 ч	90
4 ч	93
2 ч	96
1 ч	99
0,5 ч	102
0,25 ч	105
7 мин	108
4 мин	111
2 мин	114
1 мин	117
30 с	120

Не все люди одинаково реагируют на шум. Одна и та же доза шумового воздействия у одних вызывает повреждения слуха, у других — нет, у одних эти повреждения могут быть тяжелее, чем у других. Поэтому любой предел допустимого шума всегда следует оценивать исходя из числа людей (в процентах), получающих после воздействия шума повреждения более слабые, чем какой-то выбранный предел. Пределы, взятые из кодекса и представленные в табл. 5, гарантируют, что у 90 % людей указанные дозы шума вызовут остаточное понижение слуха менее чем на 20 дБ после 50 лет работы при указанной дозе шумового облучения.

При снижении пределов на 5 дБ эта цифра увеличится до 93 %, а при снижении на 10 дБ — до 96 %. Потеря слуха более чем на 20 дБ начинает серьезно мешать человеку, когда к этому добавляются еще возрастные изменения слуха. Понижение слуха меньше чем на 20 дБ не очень существенно, а на 10 дБ — практически неощутимо.

Как правило, шум, настолько громкий, что невозможно разговаривать, не переходя на крик, уже несет опасность повреждения слуха. Можно утверждать, что если человек, не работающий систематически в шумовой зоне, получит после пребывания в ней временный сдвиг порога слышимости, то уровень шума в зоне скорее всего превышает 90 дБА. Вообще, независимо от продолжительности воздействия оставлять уши незащищенными при уровне шума в 120 дБ неразумно, а при уровне, достигающем 135 дБ, — опасно. Даже при пользовании ушными протекторами абсолютный предел допустимого уровня шума составляет 150 дБА, а так как многие виды протекторов снижают уровень всего на 20 дБА или даже меньше, то ношение их не уничтожает опасности повреждения слуха, если вы находитесь весь день в зоне сильного шума. Как мы увидим в гл. 11, это не единственный недостаток ушных протекторов, препятствующий решению проблемы повреждения слуха шумом.

По-видимому, шумы, состоящие из чистых тонов, более опасны, чем широкополосные шумы; поэтому на заводах, где машины или какие-либо процессы производят шумы одного тона или группы тонов очень большой громкости, предельные уровни шума должны быть на 5—10 дБА ниже, чем это предусмотрено кодексом.

Понижение слуха, вызванное производственным шумом, иными словами, профессиональное повреждение слуха, — пожалуй, самое серьезное воздействие шума, но оно не единственное. Шум оказывает на человека много других вредных воздействий: некоторые виды шума и вибрации вызывают заболевания; шум может серьезно нарушить связь, он нередко приводит к несчастным случаям; при постоянном раздражающем воздействии шум может вызвать психические нарушения; шум мешает заснуть и прерывает сон, и результаты этого могут быть весьма серьезными.

Короче говоря, шум ухудшает условия жизни человека.

Еще не все вредные воздействия шума и его сообщника— вибрации раскрыты до конца. Известно, что люди, работающие с вибрирующими ручными инструментами, страдают заболеваниями, известными как «белые пальцы», «мертвая рука», «явление Рейно». Симптомы заболевания — боль, онемение и цианоз пальцев, как при действии холода. Очень часто наблюдается и повреждение суставов и костей рук, причем суставы распухают и теряют подвижность. Возможно, что повреждения костей и суставов наступают в результате повторных резких ударов, которым подвергаются кисти рук при работе с ударными механизмами, а другие симптомы вызываются высокочастотными колебаниями. Есть у меня такая, казалось бы, невинная машинка — ручной пылесос для автомобиля, совершающий вибрации с частотой 290 Гц. Уже через полчаса работы он вызывает онемение и слабое покалывание в руке. Я обнаружил также, что вибрация кисти может вызвать временный сдвиг порога слышимости вследствие передачи колебаний через кости руки и шеи во внутреннее ухо. На сей раз виновником оказался ручной вибрационный гравировальный резец с частотой вибраций 50 Гц. Поработав этим резцом в течение получаса и надев ушные протекторы, чтобы исключить возможность сдвига порога звуком, передающимся по воздуху, я нашел у себя временный сдвиг порога, эквивалентный сдвигу, возникающему при том же времени воздействия высокочастотного шума в октавной полосе с уровнем около 90 дБ. Если подобный инструмент может привести к временному сдвигу порога, он, несомненно, может вызвать и остаточное понижение слуха у людей, работающих с ним постоянно. Наиболее вредное действие обычно оказывают гармоники рабочей частоты механизма, а эти гармоники даже у пневматического сверла достигают нескольких кГц. Такая вибрация повреждает периферические нервы и капилляры пальцев и кистей рук.

Другие вредные воздействия шума и вибраций на организм в настоящее время не считаются серьезными, за исключением воздействия звуков очень высоких или очень низких частот, а также очень большой интенсивности.

Шум очень большой интенсивности может вызвать резонанс в полукружных каналах — органах равновесия, находящихся во внутреннем ухе, что приводит к головокружению и тошноте. Ультразвуковой шум с частотой, превышающей границу слышимости, также может вызвать тошноту, а инфразвук и очень низкочастотный слышимый шум возбуждают резонансы во внутренних органах, включая сердце и легкие. Акустическим возбуждением с определенной частотой и достаточно большой амплитудой можно остановить пульсацию сердца. Сильный низкочастотный шум затрудняет дыхание.

Из-за резонансов, возбуждаемых в лицевых и черепных костях слышимыми звуками средних частот, их воздействие чрезвычайно неприятно даже при употреблении ушных протекторов: утрачивается ясность мысли, возможно, вследствие резонансных явлений, возникающих в головном мозге; нарушается координация движения конечностей, что, возможно, вызвано вибрацией мозга и периферических нервов. Если по той или иной причине человек вынужден находиться в зоне весьма интенсивного шума, он должен по меньшей мере надеть звукозащитный шлем, а не ограничиваться ушными протекторами.

Важны также психологические и другие непатологические последствия шумовых воздействий, но они не всегда поддаются измерению. Как измерить степень раздражения, испытываемого человеком? Сколько вреда приносит плохое настроение? Раздраженные люди становятся иногда неестественно вспыльчивыми или принимают совершенно неправильные решения, которые подчас могут привести к катастрофическим последствиям. У жертв шума может развиться депрессия или склонность к психосоматическим заболеваниям; разрушаются семьи, возникают несчастные случаи, осложняются отношения на производстве.

Шум вызывает и обычную усталость и неспособность сосредоточиться, также ведущие к снижению производительности труда и несчастным случаям. Измерить зависимость производительности труда от шума не просто: как только мы отбираем группу обследуемых и начинаем экспериментировать, изменяя окружающие условия, будь то акустика, освещение или отопление, — производительность труда испытуемых немедленно возрастает просто от того, что они ощущают заботу о своем здоровье и стремление как-то им помочь.

Однако мало кто решится отрицать, что люди, работающие в условиях сильного шума, чаще ошибаются и, следовательно, их труд менее производителен и эффективен. Установлено также, что при снижении уровня шума уменьшается число невыходов на работу.

Вероятно, расстройство сна — самый серьезный ущерб, который шум приносит человеку, исключая, конечно, повреждения слуха. Для эффективной работы, умственной и физической, почти всем нужен полноценный сон. Следует помнить, что, когда человек спит, его органы чувств, в том числе и уши, остаются «включенными». Если во время сна мы не слышим звуков низкого уровня, то это вовсе не значит, что уши не улавливают их, а просто головной мозг иначе реагирует на слуховые раздражители. Как известно, даже под наркозом нервные импульсы продолжают передаваться в высшие центры головного мозга. Шум низкого уровня может не оказывать видимого влияния на сон, но факт восприятия шума выявляется при внимательном анализе электроэнцефалограммы (ЭЭГ). Во время глубокого сна щелчок в 50—60 дБА вызывает легко идентифицируемый ответ коры головного мозга. Любопытно, что метод ЭЭГ позволяет осуществить аудиометрию даже помимо желания исследуемого, так как ответы коры совершенно непроизвольны. Шумы более высоких уровней вызывают весьма выраженные изменения ЭЭГ.

Проще всего считать, что влияние шума на сон сводится к тому, что под действием шума человек пробуждается. Разумеется, это очень важный момент, но многие недооценивают значения вынужденного сдвига глубины сна, еще не приводящего к пробуждению. Как показывают эксперименты, если на спящего человека, едва достигшего стадии самого глубокого сна, воздействовать так, чтобы, не разбудив, перевести в стадию менее глубокого сна, результат оказывается таким же, как и при полном пробуждении.

Внезапное пробуждение от глубокого сна может сопровождаться сердцебиением. Если человека будить каждый раз, когда он доходит до стадии сновидений (легко определяемой по быстрым движениям глаз), и таким образом лишить снов, у него развиваются симптомы, приводящие в конце концов к галлюцинациям и дезориентации.

Шум вызывает как сдвиги глубины сна, так и полное пробуждение. Хорошо известно, что людей в возрасте старше 60 лет легче разбудить или перевести в состояние менее глубокого сна, чем детей или людей среднего возраста. Различия в реакции резко выражены; установлено, что шум, который будит лишь 5 % детей 7—8-летнего возраста, вызывает полное пробуждение 70 % людей в возрасте 69—72 лет. Разбуженный пожилой человек труднее засыпает вновь, чем ребенок или человек средних лет. Доказано также, что женщины легче просыпаются от шума, чем мужчины.

Если сопоставить изменения сна, вызываемые шумом, с нормальным процессом сна, легко понять, как значительна роль окружающего шума. Известно, что для спящего наиболее благотворна стадия глубокого сна, а для того чтобы достигнуть ее, взрослому человеку требуется около часа, и очевидно, что нескольких кратковременных шумовых раздражений в течение ночи достаточно, чтобы вызвать серьезное расстройство полноценного сна. Такое же значение имеет и стадия сновидений, частые пробуждения во время которой могут сильнейшим образом отразиться на качестве сна.

Исследовалось также вторичное проявление действия окружающего шума на сон, а именно удлинение срока, необходимого для наступления стадии глубокого сна. В одном эксперименте было обнаружено, что в условиях тишины между моментом, когда человек ложится в постель, и наступлением глубокого сна проходило в среднем 26 мин, а при наличии транспортного шума это время составляло более 50 мин, В известных пределах головной мозг способен компенсировать нарушения качества сна в условиях шума и недостаток глубокого сна в начале ночи возместить увеличением продолжительности стадии глубокого сна и большей его устойчивостью в более поздние часы (порядок, обратный нормальному).

Если говорить о пределах допустимого ночного шума, то следует заметить, что шум постоянного уровня меньше влияет на сон, чем шум с колебаниями уровня или прерывистый шум.

Значит, важнее попытаться предотвратить несколько коротких «вспышек» шума, чем стремиться понизить общий шумовой уровень. Здесь, как и в других ситуациях, наличие подходящего фона может оказать действенную помощь в случаях, когда нельзя избежать прерывистого шума большого уровня. В тропиках, где вделанные в окна шумные устройства для кондиционирования воздуха распространены очень широко, человеку, безусловно, гораздо легче спать, если такое устройство не управляется терморегулятором, а работает непрерывно.

При фоновом шуме в 35 дБА отдельные шумовые максимумы с уровнем в 45—50 дБА, хотя и кажутся слишком высокими, практически вполне приемлемы для 80 % спящих людей; при увеличении числа шумовых максимумов этот предел следует понизить.

Наконец, шум порождает еще одну проблему — нарушение связи. Во многих житейских ситуациях очень важно, чтобы один человек мог быстро и точно передать информацию другому. Тысячи лет устное слово было основным средством связи, и, хотя сейчас развитие электроники несколько снизило эту его роль, речь по-прежнему чрезвычайно важна для всех нас. Нарушение связи может привести, во-первых, к снижению эффективности труда и, во-вторых, к гораздо более серьезным и даже фатальным последствиям. Нередко несчастные случаи можно предотвратить окриком: «Поберегись!» (если прохожему грозит, например, опасность свалиться в яму) или более длинным предостережением: «Провода под током!». Очевидно, если окружающий шум помешает услышать такие предостережения, люди погибнут по причинам, предотвратить которые было возможно.

Таблица децибел

Пример: сложение шумов суровнями 86, 83 и 79 дБ, ответ: 1,0 + 0,5 + 0,2 = 1,7, что соответствует примерно 2 дБ, так что суммарный уровень составляет 88 дБ.

Отношение интенсивностей	дДБ	Отношение интенсивностей	дБ
100	+20	0,80	?1
79	+ 19	0,63	?2
63	+ 18	0,50	?3
50	+ 17	0,40	?4
40	+ 16	0,32	?5
32	+ 15	0,25	?6
25	+ 14	0,20	?7
20	+ 13	0,16	?8
16	+ 12	0,13	?9
13	+ 11	0,10	?10
10	+ 10	0,079	?11
7,9	+9	0,063	?12
6,3	+8	0,050	?13
5,0	+7	0,040	?14
4,0	+6	0,032	?15
3,2	+5	0,025	?16
2,5	+4	0,020	?17
2,0	+3	0,016	?18
1,6	+2	0,013	?19
1,3	+ 1	0,010	?20
1,0	0

Воздух, волны, звук

Разумеется, шум — это просто один из видов звука. Обычно шум называют «нежелательным звуком», что в известной мере справедливо. Но то, что для одних ушей — шум, для других — музыка. Рев самолета, проносящегося над крышей дома, невыносим для несчастного жильца. Но как он радостен для жены летчика-испытателя, возвращающегося из первого полета! Так или иначе, всякий шум — это звук, и, прежде чем пускаться в изучение сложных методов ослабления шума, необходимо как следует понять, что же такое звук вообще.

Удивительно, что многие люди, изучавшие еще в школе звук, колебания и волны, сохранили впечатление, что волнистые линии на картинке в учебнике дают как бы «портрет» звуковой волны и что воздух заполнен невидимыми волнистыми линиями, исходящими от каждого источника звука. Все это, конечно, не так, и мы не сможем двигаться дальше, не уяснив природу звука.

Звук можно создать в любой среде. Мы привыкли наблюдать его в воздухе, но его можно обнаружить и в воде, и в бетоне и практически в любом твердом веществе, в любой жидкости, в любом газе; звука не может быть только в пустоте. Таким образом, прежде всего нам следует поговорить о свойствах среды, а так как большая часть звуков, которые мы слышим, приходит из воздуха, то в качестве примера нам лучше всего взять именно воздух. Если кому-либо трудно представить себе, что звук может приходить не только из воздуха, пусть он прижмет свои ручные часы ко лбу: если вокруг тихо, то при достаточно остром слухе он услышит тиканье, звуки которого, минуя воздух, прошли через металл часовой крышки и кости черепа.

Воздух упруг. Если эти слова вызывают у нас ассоциацию с резиной, а сходства между воздухом и резиной, как мы отлично знаем, никакого нет, то следует забыть привычный смысл этого слова и вспомнить, что, когда сжимают какой-либо объем воздуха, например в велосипедном насосе, воздух всегда стремится вернуться к прежнему состоянию.

Именно это и означает слово «упругий»: если деформировать упругое тело, оно сопротивляется деформации и стремится восстановить свое исходное состояние. Свойство, обратное упругости — пластичность. И здесь опять же нужно представлять себе не пластмассовую миску для мытья посуды, а какое-либо вещество, которое после деформации сохраняет вновь приобретенную форму. Материал, из которого сделана миска, потому и называют пластмассой, что он «термопластичен», то есть обладает пластичностью в горячем состоянии (при охлаждении она утрачивается). Чтобы среда могла проводить звук, она должна быть упругой; в отсутствие упругости в среде невозможно волновое движение, которое и есть звук.

Предположим, желая привлечь внимание какого-то человека, я бросил в него камешек. Если человек особенно нечувствителен и первый камешек не произведет впечатления — я могу бросить второй. Если человек решил не обращать внимания на мои выходки, то, вероятно, запас камней у меня скоро кончится. Но я могу применить более экономный способ обратить на себя внимание, — а именно, ткнуть в человека палкой. Преимущество этого способа заключается в том, что после каждого тычка палка остается у меня, и я смогу продолжать свои попытки до тех пор, пока либо не заставлю его взглянуть на себя, либо не получу сдачи! Замечательно, что эти два способа приставать к человеку принципиально различны действуя с равными силами, я могу одинаково ушибить человека обоими способами, но, бросая камни, я передаю не только силу, но и множество камней, а вот когда я толкаю человека палкой, то не передаю ничего, кроме силы! Замечательно: уже удалось наставить человеку синяки, а палка как была у меня, так и осталась! При этом от меня к нему не перешло ничего, кроме энергии. Точно так же, когда мы слышим издалека шум летящего самолета, мы получаем от него только малое количество энергии, но никакие частицы воздуха от самолета к нам не долетают, и никакие волнистые линии не устремляются сквозь воздух.

В этом суть волнового движения.

Следует отметить еще одно обстоятельство: когда человека толкают палкой, она попеременно то прикасается к его руке, то отходит от нее, скажем, на 100 мм. Она колеблется вперед-назад, вперед-назад, и такое колебание — еще одно неотъемлемое свойство волнового движения.

Однако мы еще не выяснили, почему упругость среды имеет столь существенное значение и каким образом энергия передается на расстояния гораздо большие, чем 100 мм, и притом с огромными скоростями.

Любое вещество — твердое, жидкое или газообразное — состоит из миллионов и миллионов крошечных молекул, расположенных, казалось бы, вплотную друг к другу. В действительности, однако, расстояния между молекулами не так уж малы по сравнению с их размерами, и молекулы удерживаются на этих расстояниях друг от друга благодаря действию сил, которое можно сравнить с действием пружин. Твердое вещество отличается от жидкости или газа только тем, что его молекулы образуют более или менее неизменную конфигурацию, а действующие между ними молекулярные силы велики. Однако в твердом веществе молекулы также отнюдь не остаются неподвижными — они непрерывно колеблются на «пружинах», связывающих их друг с другом. Чем более нагрето твердое тело, тем оживленнее движутся молекулы, а когда температура достигает точки плавления, твердое вещество превращается в жидкость[5]. Как в твердых телах, так и в жидкостях молекулы, находящиеся на поверхности, не имеют сверху «партнеров», с которыми они могли бы образовать молекулярные связи, но тем сильнее они связываются с ближайшими к поверхности молекулами, и это приводит к появлению поверхностного натяжения. Если продолжить нагревание, движение молекул усилится, связи их с «соседями» станут мимолетными, поверхностное натяжение исчезнет и жидкость испарится. Разумеется, испарение происходит и при температуре ниже точки кипения, потому что всегда существует некоторый постоянный поток молекул, отрывающихся от поверхности жидкости случайно.

Существенно, что, хотя молекулы газа не имеют определенных связей со своими соседями, на них все же действуют сложные силы упругого типа, которые снова свяжут их и обратят газ в жидкость или в твердое вещество, как только температура понизится и молекулы замедлятся. Молекулы нечувствительны к тому, какие именно другие молекулы становятся их соседями, но сильно реагируют на степень их близости.

Из сказанного становится ясно, каким образом твердые тела, жидкости и газы проявляют упругость при приложении напряжения — молекулы либо теснее сдвигаются, либо расходятся, а их пружиноподобные связи сжимаются или растягиваются. Как только напряжение снимается, «пружины» вернут молекулы в исходное положение равновесия. О молекулах газа правильнее сказать, что «пружины» не оттягивают их в прежнее положение, а раздвигают друг от друга на прежнее расстояние[6].

Теперь представим себе длинную, наполненную воздухом трубу, с одного конца которой вставлен поршень (рис. 1). Можно было бы предположить, что если поршень быстро вдвинуть внутрь трубы, то весь столб воздуха одновременно продвинется вперед, освобождая место для поршня. Однако произойдет нечто совсем другое. Молекулы воздуха, удерживаемые на некотором расстоянии друг от друга силами упругого типа, — это мельчайшие частицы вещества, и, следовательно, они обладают массой. Каждая молекула все-таки кое-что весит, а поскольку она обладает массой, она проявляет инерционные свойства. Припомним первый закон Ньютона: каждое тело находится в состоянии покоя или равномерного прямолинейного движения до тех пор, пока внешняя сила не выведет его из этого состояния. Например, как бы хорошо ни были смазаны петли тяжелой дубовой двери, чтобы закрыть ее, обязательно нужно приложить известное усилие, потому что из за своей массивности она как бы сопротивляется и не приходит сразу в движение Когда же она придет в движение, понадобится почти такое же усилие, чтобы ее остановить.

Рис. 1 Действие движения поршня на молекулы воздуха в трубе.

Подобным образом, но в малом масштабе сопротивляются изменению движения молекулы воздуха, ближайшие к поверхности поршня Когда поршень вдвигается, инерция не позволяет этим молекулам мгновенно прийти в движение, поэтому «пружины», отделяющие их от поверхности поршня, сожмутся. Потенциальная энергия, сообщенная поршнем этим «пружинам», заставит молекулы двигаться вперед. Придя в движение, молекулы, обладающие определенной массой, приобретут кинетическую энергию; потенциальная энергия «пружин» превратится в кинетическую энергию молекул Затем этот процесс повторится, молекулы первого слоя начнут толкать молекулы следующего слоя, вследствие инерции те также сопротивляются и приходят в движение только после того, как сожмутся «пружины», действующие между молекулами первого и второго слоев. Аналогичное явление (в гораздо более крупном масштабе) наблюдается, когда маневренный паровоз толкает на запасной путь состав железнодорожных вагонов Вследствие инерции первого вагона — и в меньшей мере трения — пружины его буферов сожмутся, и только после того, как они запасут достаточную потенциальную энергию, первый вагон начнет катиться по рельсам При этом он сожмет пружины буферов между первым и вторым вагонами и т. д.; в результате пройдет заметное время, прежде чем покатится также и последний вагон Теперь легко понять, почему при быстром вдвигании поршня в трубу на небольшое расстояние весь воздушный столб в целом не приходит в движение мгновенно каждому молекулярному слою нужно время, чтобы сдвинуть с места следующий слой. Потребуется целая секунда для того, чтобы на протяжении 344 м воздух продвинулся вдоль трубы на расстояние, пройденное поршнем. Если бы молекулы были тяжелее или молекулярные силы слабее, времени понадобилось бы больше. Расстояние в 344 м относится к температуре в 20 °С, при 0 °С оно уменьшится до 332 м (с точностью до одного метра) Такое сокращение расстояния обусловлено тем, что при охлаждении молекулы сближаются, и, если бы мы могли подсчитать число слоев молекул воздуха в столбе длиной 344 м при 20 °С, оно равнялось бы числу слоев в столбе воздуха длиной 332 м при 0 °С[7].

Хотя при охлаждении молекулы воздуха сближаются, при одном и том же атмосферном давлении упругость «молекулярных пружин» останется прежней, поскольку интенсивность движения молекул при охлаждении соответственно уменьшится

Все эти рассуждения вполне применимы и при движении поршня назад В этом случае он не сжимает «пружины», а растягивает их до тех пор, пока ближайший к нему молекулярный слой не начнет также двигаться назад Молекулы первого слоя, кинетическая энергия которых обусловлена этим движением, в свою очередь растянут «пружины», связывающие их со следующим слоем, и т. д. В результате, после того как поршень сдвинулся сначала вперед, а потом назад, все молекулы вернутся на свои исходные места; при этом они, подобно палке, передадут «толчок», не получив в итоге никакого остаточного перемещения. В сущности, воздушный столб не так уже сильно отличается от палки Если бы удалось выполнить соответствующее измерение, то оказалось бы, что и в палке для передачи «толчка» от одного конца к другому требуется несколько миллисекунд В воздушном столбе на это уходит больше времени, но толчок поршня на одном конце столба непременно передастся на другой конец; в этом можно убедиться, натянув поперек трубы тонкую мембрану. Соединим поршень с коленчатым валом и начнем колебать поршень туда и обратно. Мембрана на другом конце воздушного столба будет повторять эти колебания, хотя и с запозданием, то есть с отставанием по фазе, потому что для передачи движения поршня от одного молекулярного слоя к другому требуется время Все это можно описать иначе можно сказать, что мембрана приводится в движение звуком, издаваемым поршнем! Однако невозможно действительно изготовить достаточно маленький коленчатый вал, так как смещение молекул воздуха в звуковой волне обычно ничтожно: когда мы слышим человека, говорящего обычным голосом, перемещение частиц воздуха вблизи нашего уха равно примерно диаметру молекулы водорода.

Если труба не слишком коротка, а движение поршня не слишком медленно, каждое колебание поршня будет доходить до мембраны не раньше, чем он успеет сделать по меньшей мере одно, а возможно, и несколько колебаний Мы уже знаем, что если длина трубы равна 344 м, то для передачи на ее дальний конец движения или звуковой волны, вызванной колебанием поршня, потребуется одна секунда Если поршень колеблется, совершая 100 циклов в секунду, то он за секунду попеременно 100 раз толкает воздух вперед и 100 раз — назад.

Промежуток времени между двумя последовательными толчками составит 1/100 с; за этот период действие первого толчка распространится вдоль трубы на 3,44 м. Следовательно, если бы удалось «заморозить» воздух в трубе и тут же его исследовать, мы увидели бы ряд сгущений молекул, расположенных вдоль всей трубы с интервалом в 3,44 мм, и ряд разрежений (явление, обратное сгущению), расположенных посредине между сгущениями (рис 2).

Рис. 2. Действие повторяющихся движений поршня на молекулы воздуха в трубе

Если вместо того, чтобы «замораживать» воздух, мы могли бы проследить за отдельной молекулой, то обнаружили бы, что она колеблется точно так же, как поршень Если бы молекула, выбранная нами для наблюдения, отстояла от исходного положения поршня на 3,44, 6,88, 10,32 или любое другое число метров, кратное 3,44, ее колебания точно совпадали бы по фазе с колебаниями поршня Если бы молекула находилась точно посередине между любыми из этих точек, она двигалась бы точно противоположно движению поршня, что соответствует сдвигу по фазе на 180°, или на 3,14 (?) радиан Движение поршня, качнувшегося вперед и назад, можно рассматривать как полный цикл кругового движения. Это позволяет указывать положение любой промежуточной точки в угловой мере, пользуясь так называемым фазовым углом, выраженным в градусах или радианах (360° = 2?, или 6,28 радиан).

Теперь мы можем уже утверждать не только то, что колебания мембраны на конце трубы вызваны звуком, издаваемым поршнем, но и что частота этого звука равна 100 герц (сокращенно Гц — единица, означающая «один цикл в секунду»), а длина волны равна 3,44 м. Итак, наконец, выясняется, что представляют собой волнистые линии, о которых мы говорили выше, — это просто графики, показывающие давление воздуха — выше или ниже атмосферного — либо в различных точках, расположенных последовательно вдоль трубы в определенный момент времени, либо в определенной точке в последовательные моменты времени.

Эти линии изображают, периодическое чередование сгущений и разрежений молекул, которые и образуют звуковые волны.

Звук, бегущий по трубе, — это частный случай, но все изложенные здесь положения носят общий характер. Разумеется, на открытом воздухе звук не передается вдоль одной прямой. Вообразим вместо трубы и поршня открытое пространство и маленький круглый баллон, соединенный с насосом, как это показано[8] на рис. 3. Если воздух попеременно накачивать в баллон и откачивать из него, баллон будет расширяться и сжиматься. При расширении действие баллона на окружающие молекулы воздуха сходно с действием движущегося вперед поршня на молекулы воздуха в трубе. «Пружины», отделяющие молекулы от баллона, сожмутся, и молекулы отойдут дальше; двигаясь, они сожмут «пружины», действующие между ними и молекулами следующего сферического слоя, и т. д. При сжатии баллона этот процесс повторяется в обратном порядке. Единственное принципиальное различие между рассмотренными случаями возникновения звуковых волн состоит в том, что в трубе сжимаются или растягиваются последовательно расположенные плоские слои молекул (так как волны сжатия, бегущие вдоль трубы, — это плоские волны), тогда как вокруг баллона колеблющиеся молекулы воздуха образуют сферические слои. Это, однако, очень существенное различие, в чем мы убедимся позже, когда будем говорить о роли расстояния от источника звука. Мы показали, что частота звука совпадает с частотой колебания источника. Поршень, совершающий 100 колебаний в секунду, создает звуковые волны с частотой, равной 100 Гц. Длина звуковой волны зависит как от скорости, с которой волны сжатия бегут по трубе (скорость звука), так и от частоты колебаний источника. С увеличением частоты колебаний поршня длина волны изменяется обратно пропорционально частоте: при 200 Гц длина волны равна 1,72 м, а при 400 Гц — 0,86 м. Математически эту зависимость можно выразить так:

где ? — длина волны, c — скорость звука, f — частота.

Рис. 3. Действие пульсирующего баллона на молекулы воздуха.

Частота звука обычно представляет больший интерес, чем длина волны. Как мы увидим в следующей главе, высота звука для слушателя определяется в основном частотой, и, если длина волны изменится (например, в результате изменения температуры), высота звука останется прежней. Нота с частотой 1000 Гц будет звучать на Северном полюсе так же, как и в пустыне Сахара. Если вы смогли бы сыграть на трубе и в Арктике, и в Африке, то звуки получились бы разные, но только потому, что изменение скорости звука изменит резонансные частоты трубы.

Единственное, что может изменить высоту звука от источника, колеблющегося с постоянной частотой, — это изменение относительной скорости источника и слушателя. Наверное, многие замечали, как резко падает высота звука мотора проносящегося мимо автомобиля. В действительности ни с приближением, ни с удалением автомобиля частота излучаемого звука не меняется. Но представьте себе, что вы стоите около ленточного транспортера, движущегося со скоростью 1 м/с, на котором установлены ящики. Грузчик ставит ящики на транспортер по одному в секунду, так что они проходят мимо вас также по одному в секунду. Если грузчик начнет двигаться по направлению к вам со скоростью, скажем, 0,5 м/с, то относительно него скорость движения транспортера уменьшится до 0,5 м/с. Если на ходу он будет продолжать ставить ящики на транспортер с прежней частотой — по одному в секунду, окажется, что расстояние между ящиками составит только 0,5 м. Следовательно, теперь ящики будут проходить мимо вас вдвое чаще, чем грузчик ставит их на транспортер. Если бы грузчик удалялся от вас со скоростью 0,5 м/с, создалась бы обратная ситуация.

Точно так же, если источник испускает звуковые волны с частотой 100 Гц и эти волны бегут со скоростью 344 м/с, вы услышите звук частотой 100 Гц.

Если источник приближается к вам со скоростью, предположим, 34,4 м/с, длина звуковой волны уменьшится на 10 %. За 1 с до вас будет доходить на 10 % больше звуковых волн, и, следовательно, вы услышите звук частотой 110 Гц; если источник звука с такой же скоростью удаляется, до вас дойдет на 10 % меньше звуковых волн и вы услышите звук частотой 90 Гц[9]. Это явление называют эффектом Доплера, оно играет большую роль, в частности в астрономии, где по «смещению Доплера» в электромагнитном спектре звезд измеряют скорости их движения.

Мы должны познакомиться с еще одним очень важным свойством звуковой волны — ее формой. Вернемся к волнистой линии, то есть к графику распределения звукового давления в какой-то определенный момент в точках, расположенных последовательно вдоль направления движения волны, или в фиксированной точке в последовательные моменты времени. Рассмотрим звук постоянной частоты, например 1000 Гц. Что за график мы получим? Разделив скорость звука на частоту, можно определить длину волны, а мы уже знаем, что звук одной частоты состоит из правильных чередований сгущений и разрежений. Какую же форму имеет волна во всем интервале? Будем искать простейшую форму повторяющегося движения. Первое, что приходит в голову, — это вращение, но оно не разрешит стоящей перед нами задачи: движение по кругу не применимо к движению частиц вперед-назад по прямой линии. А может все-таки применимо? Если вращать гирьку, подвешенную на веревке, и смотреть на нее сбоку, мы увидим не вращение гирьки, а только ее движение вверх и вниз. Глядя таким образом, мы обнаружим, что смещение гирьки от центра изменяется как синус угла, описываемого веревкой. Такое движение называют «синусоидальным»: этим указывают, что оно изменяется подобно тригонометрической функции — синусу.

Синусоидальное движение чаще называют простым гармоническим движением (ПГД), и звуковая волна, испускаемая источником, совершающим колебания типа ПГД, является самым чистым звуком из возможных и единственным видом волны одной — единственной частоты.

Возвращаясь к нашей волнистой линии, мы без труда обнаружим, что она имеет синусоидальную форму. Существуют веские, хотя и сложные математические обоснования того, почему синусоидальные колебания представляют собой самый важный вид осцилляции, или колебаний. Любое упругое тело, совершающее свободные колебания, создает именно синусоидальные волны. Однако очень редко тело колеблется так правильно, что порождает только одну беспримесную синусоидальную волну; обычно к такой синусоидальной волне присоединяется целый ряд других волн меньших амплитуд.

Поэтому чистые тоны встречаются на практике очень редко — почти все звуки, которые мы слышим, гораздо сложнее и состоят из большого числа тонов, звучащих одновременно. Как это отражается на графике? Ответ на этот вопрос дает самая простая арифметика, но более научно звучит термин «метод суперпозиции». Чтобы вычертить график давления звуковой волны, которая состоит из двух или более простых тонов, или синусоидальных волн, достаточно сложить (или вычесть) соответствующие значения давления каждой волны в каждой точке и результат нанести на чертеж. Таким путем можно комбинировать любое число простых волн, получая в итоге волны очень интересной формы. Результирующая форма волны зависит не только от частот составляющих синусоидальных волн, но также и от соотношения между их амплитудами и фазами.

Хотя на первый взгляд это представляется невероятным, но в действительности любую непрерывную периодическую волну можно представить в виде суммы ряда синусоидальных волн соответствующих частот и амплитуд. Первым это доказал французский ученый Ж. Фурье, когда он разрабатывал теорию распространения тепла. Однако его книга «Аналитическая теория тепла», опубликованная в 1822 г., приобрела гораздо более общее значение благодаря очень существенной теореме, в ней содержащейся. Полностью теорема Фурье звучит так: каждое конечное и непрерывное периодическое движение можно разложить в простой ряд синусоидальных волн с соответственно подобранными фазами и амплитудами.

В дальнейшем эта теорема окажется нам чрезвычайно полезной, и поэтому важно понять ее точный смысл. Рассмотрим ее на простейшем примере прямоугольной волны (рис. 4), хотя такие волны встречаются не в акустике, а в электронике. Глядя на рис. 4, трудно вообразить, что эту столь отличную от синусоидальной волну можно представить в виде ряда синусоидальных волн. Тем не менее это возможно, правда, в виде бесконечного ряда. Если, как показано на рис. 4, начать построение компонент с синусоидальной волны той же частоты, что и прямоугольная волна, но несколько большей амплитуды и затем прибавить волну утроенной частоты с амплитудой, равной одной трети первой волны, то прямоугольная форма начнет выявляться. Далее прибавим синусоидальную волну пятикратной частоты и амплитуды, равной одной пятой от амплитуды первой волны, и т. д.; когда мы дойдем до волны с пятнадцатикратной частотой и амплитудой, в пятнадцать раз меньшей, чем амплитуда первой волны, то форма результирующей станет очень похожей на исходную прямоугольную волну. Интересно отметить, что если график анализируемой волны содержит крутые изгибы и изломы (например, прямые углы рассмотренной выше волны), то высокочастотные компоненты ряда Фурье будут иметь значительно большие амплитуды, чем для волны более плавных очертаний.

Как это ни представляется странным, но точно тем же способом, каким мы производили построение прямоугольной волны из ряда синусоидальных волн, можно осуществить и обратное — разложить в подобный ряд любую конечную, непрерывную и периодическую волну. Полностью значение этого обстоятельства выяснится позже.

Разумеется, воздух не единственный передатчик звуковых волн, и практически любой газ, твердое тело или жидкость ведут себя подобным же образом и тоже могут передавать звуковые волны. Но хотя основные законы распространения звука в разных средах одни и те же, такие величины, как, например, упругость и плотность среды, различаются в широких пределах, что прежде всего отражается на скорости звука.

Так, в большинстве твердых тел скорость звука по крайней мере втрое больше, чем в воздухе. Это связано с тем, что скорость звука пропорциональна корню квадратному из отношения соответствующего коэффициента упругости к плотности среды. Чем больше это отношение, тем больше скорость звука. В алюминии скорость звука при 15°С равна 5200 м/с, то есть более чем в 15 раз превышает скорость звука в воздухе; в стали при той же температуре скорость звука равна 5050 м/с. Если мы приложим ухо к одному концу длинной стальной трубы, то при ударе по другому ее концу сначала услышим ухом, приложенным к трубе, удар, переданный металлом трубы, а потом другим ухом — второй удар, принесенный волной, прошедшей через воздух. Эта вторая волна на прохождение того же расстояния затратит в 15 раз больше времени.

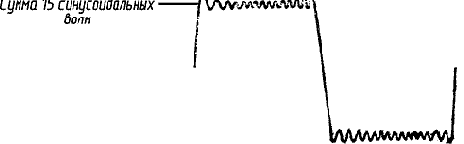Рис. 4. Формирование волны прямоугольной формы

Акустики прошлого века приняли этот метод для определения скорости звука в твердых телах; предварительно они нашли скорость звука в воздухе, измеряя время между наблюдением вспышки и приходом звука от взрыва, происшедшего на большом расстоянии. Затем достаточно было измерить промежуток времени между двумя приходами звука от удара, произведенного по дальнему концу очень длинной трубы или бруса. Первым произвел такое измерение в 1808 г. француз Био, который воспользовался чугунной трубой длиной в целый километр. Чтобы на таком расстоянии расслышать звук, приходящий по воздуху, пришлось на дальнем конце трубы закрепить колокол. Сходный, но более трудный эксперимент произвели физики Колладон и Штурм для определения скорости звука в воде. На Женевском озере они опустили под воду колокол и одновременно с ударом по нему взрывали небольшой заряд пороха. При этом они измеряли время между моментом появления вспышки и приходом звука от колокола. Во всех этих опытах время измерялось с помощью секундомера, и поэтому результаты были не слишком точны. При измерении гораздо более тонкими методами скорость звука в пресной воде при 15° оказалась равной 1440 м/с.

В дальнейшем мы увидим, что во многих проблемах шума звук, распространяющийся в твердых телах, играет ничуть не меньшую роль, чем звук, бегущий в воздухе; в частности, внутри зданий заметная доля шума часть своего пути проходит в твердом теле. Частота одного и того же звука в твердом теле и воздухе всегда одинакова, но вследствие большей скорости звука в твердых телах длина звуковой волны в них гораздо больше, чем в воздухе Впрочем, длина звуковой волны в твердых телах обычно представляет интерес только при вычислении резонансных частот в конструкциях.

&nbsp

[5] Некоторые твердые вещества сублимируют — непосредственно переходят из твердого состояния в пар: таковы, например, йод и сухой лед (твердая углекислота).

[6] Следует иметь в виду, что, обсуждая поведение молекул под действием звука, автор нигде не учитывает тепловое движение молекул. По существу, речь идет не о молекулах, а о частицах среды, содержащих множество молекул. — Прим. ред.

[7] Здесь автор допускает ошибку число слоев обратно пропорционально квадрату скорости звука, а не первой степени — Прим. ред.

[8] На этом рисунке масштаб не соблюден: размеры баллона в поперечнике должны быть много меньше длины звуковой волны. — Прим. ред.

[9] Здесь автор допускает ошибку: при движении источника звука со скоростью v вдоль прямой, соединяющей источник и приемник, слышимая частота f ' равна частоте f испускаемого звука, деленной на (1 ? v/c) или на (1 + v/c), в зависимости от того, приближается или удаляется источник, соответственно. В рассмотренном случае слышимый звук будет иметь частоту 111 Гц при приближении источника и 91 Гц при его удалении. Формула f ' = f (1 ± v/с), примененная автором, справедлива для случая движения приемника, а не источника. При малых по сравнению со скоростью звука скоростях движения разница между этими случаями мала. — Прим.Ред.

о том, что нам приходится

Нужно ли писать книгу о том, что нам приходится мириться со слишком большим шумом? Остановитесь и прислушайтесь! Но недостаток знаний о самом шуме ощущается во всем: мало кто знает, что такое шум, как он на нас действует и, самое важное, как избежать его создания.
Люди привыкли к разговорам о децибелах, хотя и не понимают, что это такое, а как бы в отместку за попытку непосвященных проникнуть в тайный мир эксперта по шумам возник целый набор новых специальных технических терминов. Такие символы, как L10 и Lэкв, вписаны в правительственные постановления и кодексы правил, но даже составителям подобных документов смысл этих символов до конца не ясен.
В наше время пользоваться советами консультанта по шумам — уже не причуда. Большие промышленные компании начинают включать в свой постоянный штат специалистов по акустике, надеясь с их помощью добиться снижения шума производимых ими механизмов; однако до сих пор и инженерам, и архитекторам случается производить акустические монстры. Сейчас уже появились ученые степени по акустике, сотни студентов окончили соответствующие вузы и аспирантуру, но людей, располагающих практическими сведениями по акустике, по-прежнему не хватает.
Люди начинают понимать разницу между двойными оконными рамами для теплоизоляции и рамами для звукоизоляции, но продолжают налепливать акустические плиты на стены и потолок, тщетно надеясь «спрятаться» от шума.
Эта книга — попытка принести свет тем, для кого все, связанное с акустикой, покрыто мраком; попытка объяснить, как шум возникает и как с ним можно бороться. Книга в равной мере предназначена как для профана, страдающего от шума, так и для архитектора и инженера, а также для всех, кто сам захочет избрать акустику своей специальностью.

Звуконепроницаемость— разоблаченный миф

«Звуконепроницаемость» — какое великолепное слово! Инженеров-акустиков всегда просят обеспечить звуконепроницаемость. Ведь водонепроницаемая обшивка не пропускает воду, так почему бы не существовать специальной обшивке, которая бы не пропускала звук? Так как роль отверстий в акустических плитках огромна, у инженеров возникла сплошная путаница между понятиями поглощения и изоляции звука. И не удивительно, потому что вопрос не прост. В предыдущей главе мы самым подробным образом объяснили, что устанавливать тонкий пористый мат с целью задержать звук, идущий из одной точки в другую, — это просто потеря времени. Максимум, чего можно добиться таким путем, — это снизить уровень на 3 дБ на высоких частотах.

Конечно, пористые материалы поглощают звук, а так как они частично уменьшают энергию звука, они уменьшают и энергию волны, проходящей через них. Но для того чтобы получить мало-мальски стоящее затухание, толщина слоя поглощающего материала должна быть сравнима с длиной звуковой волны. Так как на практике часто приходится иметь дело со звуковыми волнами длиной в несколько метров, ясно, что об использовании поглощающих материалов непосредственно в качестве звукоизоляторов не может быть и речи. Что же применить в таком случае? Из какого вещества изготовить «звуконепроницаемость»? По-видимому, требуется нечто необыкновенное, поскольку вполне разумное значение звукоизоляции 40 дБ означает, что интенсивность звука нужно уменьшить в десять тысяч раз!

Вернемся назад и снова внимательно присмотримся к тому, что происходит, когда звуковая волна падает на некоторую поверхность. Обычно большая часть звуковой энергии отражается, некоторое количество ее поглощается и переходит в тепло, а часть проникает через поверхность. В силу закона сохранения энергии в каждом случае сумма всех этих долей энергии: отраженной, поглощенной и прошедшей — всегда должна равняться энергии волны, падающей на поверхность.

Так как нам желательно уменьшить долю прошедшей волны, логично попытаться увеличить долю отраженной или поглощенной волны. Но увеличить поглощение нельзя: это требует большого объема и дорогих материалов (кроме случая высоких частот); поэтому остается только увеличивать интенсивность отраженной волны за счет прошедшей.

В такой постановке проблема упрощается: чем больше отражает поверхность, тем меньше звука проникает через нее. В предыдущей главе мы рассмотрели условия отражения звука. Так, гранитная стена настолько массивна и так мало сжимаема, что легкие молекулы воздуха не могут оказать на нее заметного воздействия. Для дальнейшего нам было бы полезно располагать некоторой мерой, которая одновременно учитывала бы и упругость, и плотность вещества. Вспомнив, что скорость звука в среде зависит от упругости и плотности этой среды, в качестве такой меры мы можем выбрать волновое сопротивление среды. Понять значение этой величины несложно. Плотность гранита велика, а вследствие его малой сжимаемости скорость звука в нем также велика. Поэтому волновое сопротивление гранита огромно. В результате этого, как мы уже знаем, при падении звуковой волны из воздуха на гранитную стену отражается больше 99 % падающей энергии. Но если бы мы заменили гранитную стену «стеной» воздуха, скачка от малого к большому импедансу не было бы, а потому исчезло бы и отражение. Чем больше различие (несогласование) импедансов двух сред, тем больше отражение и тем меньшая доля падающей волны проходит из одной среды в другую.

Однако около 1 % звуковой энергии все же входит в гранит, и, поскольку стена не бесконечно толстая, часть энергии, которая проникла в гранит и не поглотилась в нем, дойдет до второй границы стены. Теперь возникает вопрос о переходе звука из гранита снова в воздух. Поскольку импеданс гранита велик, ничтожные смещения его частиц уже создают высокие давления в волне; однако эти же смещения создадут в воздухе лишь весьма малое давление.

Поэтому волна, распространяющаяся в граните, при падении на его границу с воздухом создаст в воздухе волну весьма малой интенсивности: передача энергии снова будет малоэффективна.

Толстая, плотная каменная стена — наилучший простой изолятор звука. На высоких частотах кирпичная стена толщиной всего 350 мм обеспечивает снижение звука более чем на 60 дБ. Однако целесообразно ли добиваться звукоизоляции, возводя тяжелую каменную стену толщиной во много десятков сантиметров? Это можно делать только в самом крайнем случае. Обычно строят стены настолько тонкие, что обе их стороны движутся почти синфазно, поскольку толщина стены мала по сравнению с длиной волны. Тогда задача о распространении звука в материале стены перестает интересовать нас, а поведение звуковой волны принимает другой характер.

Представим себе тонкую панель или перегородку площадью 3 м2, имеющую опору, но не закрепленную по периметру. Если с одной стороны приложить к ней постоянное давление, она прогнется, и величина прогиба будет целиком определяться ее упругостью (жесткостью). Так, резиновая панель сильно выгнется, тогда как стальная едва поддастся. Если давление на. одну сторону будет медленно переходить от положительного к отрицательному, возникающие выпучивание и выгибание панели по-прежнему будут определяться ее упругостью. Однако поскольку панель обладает инерцией, при достаточном увеличении частоты знакопеременного давления ее масса начнет сказываться в той же степени (а затем и больше), что и упругость. Представим себе дверь, подвешенную на упругих петлях. Если попытаться медленно покачивать дверь вперед-назад, ее движение в основном будет ограничиваться упругостью подвески. Если же начать быстро дергать дверь туда и обратно, то главную роль начнет играть ее инерция: фанерную дверь гораздо легче раскачивать, чем дубовую, даже если упругость петель не изменилась.

Рис. 39. Изменение смещения, скорости и ускорения панели от времени
(при двух частотах колебания, справа частота вдвое выше, чем слева).

Поэтому говорят, что на очень низких частотах передача звука через панель управляется ее упругостью, но по мере роста частоты инерция (масса) становится значительно более существенной. Поясним это на примере, когда возбуждающая сила — синусоидальный звук (чистый тон). В этом простейшем случае смещение панели синусоидально. Мы уже знакомы с графиком синусоидальной функции. Скорость изменения положения — это скорость, скорость же изменения скорости — ускорение. На рис. 39 показаны графики смещения, скорости и ускорения для панели, колеблющейся на некоторой определенной частоте, а также на частоте вдвое большей. При данном звуковом давлении с увеличением частоты смещение убывает по амплитуде, но скорость частиц остается без изменения. Далее, на рисунке видно, что при этом скорость изменения скорости стала вдвое больше: максимальное значение ускорения удваивается при удвоении частоты. Но, согласно второму закону Ньютона, ускорение прямо пропорционально приложенной силе. Таким образом, теоретически при удвоении частоты потребовалась бы вдвое большая сила, чтобы заставить панель колебаться с той же скоростью. Однако, так как действующая со стороны звуковой волны сила не изменилась, удвоение частоты звука приведет к уменьшению амплитуды колебаний панели вдвое.

По другую сторону от панели картина такова, как если бы источником звука была панель. Звук, падающий с одной стороны, приводит ее в колебания, и эти вынужденные колебания излучают с другой стороны звуковые волны — ослабленные копии падающих волн. Поскольку при удвоении частоты амплитуда скорости уменьшается вдвое, можно ожидать, что звуковое давление излучаемых с другой стороны волн также уменьшится вдвое. Теоретически так и есть. Вспоминая, что при уменьшении звукового давления, вдвое уровень его уменьшается на 6 дБ, приходим к заключению, что удвоение частоты увеличивает звукоизоляцию на 6 дБ.

Как мы знаем из второго закона Ньютона, ускорение обратно пропорционально массе тела.

Отсюда следует, что при данной частоте звукоизоляция панели увеличивается на 6 дБ при каждом удвоении массы панели. Однако это чисто теоретические рассуждения, и, как мы скоро увидим, на практике возникает множество обстоятельств, в результате которых поведение панели не следует этому «закону масс». Вместо улучшения изоляции на 6 дБ в самом лучшем случае удается добиться не более 4—5 дБ. Эмпирически полученный «закон масс» выглядит, как показано на рис. 40.

Рис. 40 Закон масс

Какие же ловушки подстерегают проектировщиков при создании звукоизолирующих перегородок? Если руководствоваться исключительно законом масс, то можно встретиться с весьма неприятными сюрпризами. Всякая перегородка обладает не только массой, но и упругостью. Хотя мы видели, что звукоизоляционные свойства перегородки определяются ее упругостью лишь на очень низких частотах, это не значит, что в других случаях упругость не играет роли. Вспомним медные тарелки из гл. 3, они резонируют именно вследствие своей упругости. От мягкой тарелки не было бы никакого проку. А перегородка, находящаяся под постоянным односторонним давлением? Величина ее прогиба определяется ее упругостью Если давление внезапно снять, перегородка выгнется в обратную сторону, и это произойдет тем быстрее, чем больше упругость перегородки Приобретя скорость, она проскочит положение равновесия и успеет совершить несколько колебаний туда-сюда, прежде чем успокоится Частота этих колебаний — резонансная частота перегородки — определяется упругостью и массой перегородки Если частота падающей волны равна или близка резонансной частоте, то перегородка будет сильно раскачиваться под действием этой волны, в результате передача звука с одной ее стороны на другую будет происходить очень эффективно Поскольку перегородка может резонировать на многих частотах, становится очевидным, что закон масс сильно нарушается.

Рис. 41 Эффект совпадений ? = ?изг соответствует критической частоте

И чтобы еще более усложнить проблему, обнаруживается дополнительный тип резонансов, который также нужно принимать во внимание То, о чем только что было сказано, напоминает резонанс груза, подвешенного на пружине, с которым мы подробно познакомились в предыдущей главе Однако, говоря о медных тарелках, мы описывали резонанс, связанный с изгибными волнами, бегущими по их поверхности. А по перегородке также могут бежать изгибные волны, как показано на рис. 41 Это волны совсем другого типа, чем звуковые волны в твердой среде, но они тоже характеризуются частотой и длиной волны При наклонном падении звуковой волны на перегородку может оказаться, что длина волны звука, отсчитываемая вдоль перегородки, и длина изгибной волны на ней совпадают В этом случае перегородка также начинает усиленно раскачиваться, что сопровождается весьма эффективной передачей звука с одной стороны на другую. Из рис. 41 видно, что для данной длины изгибной волны существует такая частота падающего звука, ниже которой подобный «эффект совпадения» невозможен, так как даже при падении волны точно вдоль перегородки длина волны звука оказывается больше, чем длина изгибной волны. Эту частоту называют критической.

Рис. 42. Типичная частотная характеристика звукоизоляции однослойной незадемпфированной перегородки.
1 — затухание определяется упругостью;
2 — область резонансов;
3 — затухание определяется массой;
4 — область эффекта совпадений.

Из всего сказанного следует, что перегородка, масса которой представляется достаточной, чтобы обеспечить хорошую изоляцию звука, на самом деле вследствие эффектов резонанса и совпадения оказывается почти бесполезной на целом ряде частот. Частотная зависимость звукоизоляции такой перегородки будет выглядеть так, как показано на рис. 42: закон масс окажется выполненным лишь в узкой полосе частот в середине спектра. Что же можно сделать? Одним из способов улучшить изоляцию является попытка расширить эту центральную полосу, сдвинув резонансные частоты как можно дальше вниз, а критическую частоту — как можно дальше вверх по спектру.

Прежде всего выясним, какую роль может сыграть упругость в осуществлении этой задачи. Чем податливей пружина, к которой прикреплена масса, тем ниже собственная частота. Уменьшение упругости перегородки не только понизит ее собственные частоты, но и укоротит изгибную волну, которая снижает изолирующие свойства панели, и тем самым повысит критическую частоту. Более тонкая перегородка также имела бы более высокую критическую частоту, но при этом уменьшилась бы ее масса, что, как мы уже знаем, нежелательно.

Следующий прием — увеличение массы перегородки; это выгодно не только в силу закона масс, но также и потому, что если это можно осуществить, не увеличивая упругость перегородки, удастся также снизить резонансные частоты и поднять критическую частоту.

Существует, однако, и другой способ решить нашу проблему, и его можно использовать как независимо, так и совместно с вышеуказанными мерами. Он заключается в следующем: вместо того чтобы отодвигать резонансы и критические частоты в дальние концы спектра (где ведь также может понадобиться хорошая звукоизоляция), попытаться снизить амплитуды резонансных колебаний и волны совпадений. Потеря изоляционных свойств перегородки в результате резонанса вызвана тем, что при резонансе к энергии, полученной перегородкой от упавшей на нее волны, прибавляется энергия, приносимая все новыми волнами. Если бы эту энергию удалось каким-то образом поглотить, эффект резонанса значительно бы снизился.

Для деформации кусочка замазки или глины достаточно затратить небольшую энергию. После деформации кусочек остается в новом состоянии, не приобретая какой-либо потенциальной энергии. Куда же девалась энергия, затраченная на деформацию такого пластичного материала? Она поглотилась в результате трения между молекулами замазки или глины и обратилась в тепло. Это как раз то, что нам нужно: если покрыть резонирующую перегородку слоем какого-либо пластичного вещества вроде глины, то при каждой деформации перегородки в процессе резонансных колебаний слой также будет деформироваться и поглощать энергию.

Этим способом можно ввести затухание в колебания перегородки. Конечно, обмазывать перегородку глиной не очень-то удобно, но существует множество материалов — от смол до различных патентованных составов, — которые действуют подобным образом. На рис. 42 пунктиром показано действие вводимого таким путем затухания: в результате даже чрезмерно упругая перегородка становится пригодной для целей звукоизоляции.

Теперь мы можем сформулировать несколько положений, которыми необходимо руководствоваться при проектировании звукоизолирующих перегородок. Для всех частот, кроме самых низких, определяющими факторами являются:

1) большая масса,

2) малая упругость,

3) высокое затухание.

Конечно, многие материалы сами по себе в той или иной степени обладают внутренним затуханием, и поэтому не всегда необходимо вносить затухание извне. Например, внутреннее затухание в фанере велико — в сто раз больше, чем в стали или алюминии. Однако при равных массах фанера обладает гораздо большей упругостью, чем стальной лист. Поэтому при введении достаточного затухания, например путем нанесения демпфирующего состава, стальной лист оказывается гораздо лучше фанеры, так как его резонансные частоты ниже, а критическая частота выше. Наилучшим материалом был бы свинец: его масса значительна, упругость мала, а затухание велико. Но свинец дорог. В Приложении 1 даны величины плотности (массы), упругости и критической частоты для различных материалов. Вообще, для однослойных перегородок задемпфированный стальной лист — наилучший вариант с точки зрения стоимости, практичности и звукоизолирующих свойств.

Однако существуют изоляторы звука гораздо более эффективные, чем однослойные перегородки. Допустим, имеется задемпфированная перегородка с малой упругостью и с поверхностной плотностью 5 кг/м2 и нам требуется улучшить звукоизоляцию. Что для этого следует сделать? Если считать, что резонансы и эффект совпадений уже по возможности подавлены, то остается одна свободная переменная — масса.

Можно увеличить массу перегородки, но даже если это удастся сделать, не увеличивая ее упругости, то, как следует из закона масс, при удвоении массы нельзя рассчитывать больше, чем на 6 дБ, а практически лишь на 5 дБ. Вряд ли такое увеличение звукоизоляции оправдает двойной расход материалов. Если учесть, что улучшение на 15 дБ потребует увеличения поверхностной плотности до 40 кг/м2, то этот путь мало заманчив, особенно если увеличение веса недопустимо с инженерной точки зрения.

В начале этой главы мы говорили о роли волнового сопротивления при передаче звука. Для упрощения, обсуждая поведение тонких перегородок, мы не касались импедансов, и, возможно, напрасно, потому что, говоря о втором законе Ньютона, об увеличении ускорения или массы, мы просто иными словами повторяли соображения, относящиеся к несогласованным импедансам. Реактивным массовым импедансом (или удельным импедансом передачи) перегородки называют произведение массы перегородки на частоту. Теперь рассмотрим механизм звукоизоляции перегородки как результат несогласования импедансов между воздухом и перегородкой со стороны, откуда падает звук, и между перегородкой и воздухом с той стороны, куда звук передается.

Что произойдет, если вместо удвоения массы перегородки мы поставим позади первой вторую перегородку, оставив между ними небольшой воздушный промежуток? Суммарная масса будет вдвое больше, как если бы мы просто удвоили толщину первой перегородки, однако при этом мы ввели еще два фактора, обусловливающих нарушение согласования импедансов, — дополнительные переходы звука из воздуха во вторую перегородку и из нее снова в воздух. Поэтому можно ожидать, что двойная перегородка окажется более эффективной, чем однослойная перегородка двойной массы. Так оно и получается на самом деле. А если бы удалось раздвинуть перегородки достаточно далеко друг от друга, оставив между ними большой воздушный промежуток, то общий эффект почти равнялся бы арифметической сумме изоляций, выраженных в децибелах, создаваемых каждой из этих перегородок в отдельности.

К сожалению, обычно приходится ставить перегородки близко друг к другу и, кроме того, каким-либо образом, например шпильками, соединять их механически друг с другом. Механические соединения увеличивают импеданс воздушного промежутка по сравнению с импедансом свободного воздуха снаружи перегородки, в результате степень несогласования импедансов внутри такой перегородки уменьшается. Тем не менее двухслойные перегородки много эффективнее, чем эквивалентные однослойные, и дают выигрыш в 10 дБ и более. При этом все проблемы, связанные с резонансами и эффектами совпадений, по-прежнему остаются существенными и даже усложняются. Появляется новый резонанс: воздух между перегородками может вести себя как резонансная труба, уже описанная в этой книге, что также снижает звукоизоляцию. К счастью, нетрудно снизить резонансный эффект слоя воздуха, применив какой-либо пористый материал. Такой слой действует на воздух подобно демпферу и влияет на резонансные свойства воздушной полости так же, как демпфирующие слои на однослойную перегородку.

Можно было бы без конца увеличивать звукоизоляцию, добавляя все новые и новые перегородки. Главным фактором здесь становится степень механической изоляции одной перегородки от другой. Если между перегородками расположен пружинящий слой типа микропористой резины, вне резонансной частоты такой «пружины» все будет хорошо, а при резонансе решающую роль сыграет степень задемпфированности слоя. К сожалению, хорошее демпфирование в межперегородочном пространстве означает повышение импеданса, а поскольку импедансы перегородок высоки, следует по возможности уменьшать импеданс промежуточного слоя. Поэтому, помещая между перегородками упругий слой или упругие элементы, предпочтительнее бороться с резонансом слоя путем уменьшения резонансной частоты (уменьшая для этого коэффициент упругости слоя), а не путем применения повышенного демпфирования.

Иногда нельзя обойтись без жесткого механического соединения между перегородками.

Если воздушный промежуток узкий, а стенки тяжелые, то результирующий эффект мало отличается от изоляции, создаваемой одиночной перегородкой с той же суммарной массой. Например, двойная кирпичная стена толщиной 280 мм с воздушным промежутком внутри толщиной 50 мм и с множеством металлических связей между обеими половинками немногим лучше, чем сплошная стена толщиной 230 мм. Можно несколько улучшить положение, убирая связи и все, что может передавать колебания, например заполняющую щебенку, а воздушную полость заполнить микропористой резиной, однако, чтобы при этом изоляция заметно возросла, потребуется увеличить воздушный промежуток по крайней мере до 100 мм.

Наиболее известный пример осуществления принципа двойной перегородки — это двойные оконные рамы. И здесь, как и в других аналогичных случаях, господствует путаница. Так, двойная рама со стеклами, жестко закрепленными в раме на расстоянии 20 мм друг от друга, дает не большую изоляцию, чем рама с одним стеклом суммарной массы. Акустическая двойная рама должна удовлетворять трем требованиям:

1. Воздушный промежуток должен составлять 100 мм или более.

2. По крайней мере одно из стекол должно быть закреплено не жестко.

3. Оконные притолоки должны иметь звукопоглощающую облицовку.

Боюсь, что сказанное может повредить продаже обычных теплоизолирующих двойных рам. Жители северных стран, например Норвегии, с давних пор устанавливают двойные рамы с большим воздушным промежутком. Поэтому в этих странах проблема возрастающего транспортного шума стоит менее остро, чем в других.

Можно указать много примеров применения многослойных перегородок для целей изоляции звука. В Приложении 2 приведены данные по звукоизоляции некоторых типов перегородок и панелей. В крайних случаях, в частности для студий и акустических лабораторий, следует строить бетонное помещение, внутри которого строят второе полностью независимое бетонное помещение, подвешиваемое на податливых креплениях, так чтобы между обоими помещениями оставался большой воздушный промежуток.

К поверхностям стен прикрепляют слой звукопоглощающего материала, и твердые соединения между помещениями полностью отсутствуют. В таком помещении необходимы двери специальной конструкции, но об этом мы расскажем в гл. 13.

Другой пример — плавающий пол. Его основу составляет бетонная плита, на которую кладется мат из минеральной шерсти и пятидесятимиллиметровый настил, подкрепленный проволочной сеткой. Это одна из лучших конструкций звукоизолирующего перекрытия, при условии что мат завернут на краях и отсутствует «акустическое короткое замыкание», например при контакте с плинтусом. Такое перекрытие также весьма эффективно уменьшает передачу ударного звука с верхних этажей на нижние. Плавающие полы и изоляцию от ударного звука мы также рассмотрим в гл. 13.

Пожалуй, наиболее непроизводительный расход с точки зрения акустики — это установка жильцами акустических плиток на потолках своих квартир, с помощью которых они надеются улучшить звукоизоляцию потолков. Как мы увидим в следующей главе, небольшой эффект действительно есть, однако вовсе не потому, что уменьшается передача звука через потолок. Хотя, как мы видели, пятидесятимиллиметровый пористый мат может уменьшить интенсивность проходящего через него звука на 3 дБ, даже этот мизерный выигрыш не достигается при расположении мата на потолке. Это объясняется тем, что импеданс пористого мата имеет промежуточное значение между импедансами воздуха и основного перекрытия, и поэтому смягчает резкость скачка, создавая более плавный, переход от малого к большому значению импеданса. Поскольку в данной конструкции изоляция звука определяется, именно резкостью несогласования импедансов, наличие пористого мата приводит к увеличению количества звука, проникающего внутрь потолка. Правда, в целом изоляция не ухудшается, потому что в мате силы вязкости, действующие между волокнами или внутри пор, приводят к поглощению энергии и снижению интенсивности примерно на те же 3 дБ; в результате звукоизоляция потолка не изменяется.

Теперь рассмотрим, как повлияет отверстие в звукоизолирующей перегородке на ее звукоизоляцию. Это нужно знать, так как во многих перегородках приходится проделывать отверстия, а даже если их и закрывают, то используют для этого материал с худшими звукоизолирующими свойствами, чем стена. Так, в стенах имеются дверные проемы, а массы дверей меньше соответствующих масс стен. Хуже того, стены зачастую имеют непредусмотренные отверстия. Как же влияют отверстия и участки с худшей звукоизоляцией на результирующий эффект?

Мы много говорили об измерении звукоизоляции в децибелах, однако точно не установили, что за этим кроется. Вопрос несложен: если звукоизоляция перегородки составляет 40 дБ на частоте 1 кГц, это значит, что уровень интенсивности прошедшей волны на 40 дБ меньше, чем уровень интенсивности падающей волны. Выше мы говорили, что при колебаниях перегородки, вызываемых падающим звуком, ее заднюю сторону можно рассматривать как источник звука. В гл. 4 мы объяснили, как измерять в децибелах полный энергетический выход источника звука — уровень мощности источника. Поэтому можно суммировать весь звук, излучаемый задней стороной перегородки, и рассчитать таким образом уровень звуковой мощности. Уровень интенсивности звука, как мы знаем, это отношение соответствующих значений, выраженных в единицах Вт/м2, представленное в децибелах. Стена площадью 4 м2 излучит энергию, равную интенсивности (в Вт/м2), умноженной на 4. Конечно, складывать величины, выраженные в децибелах, следует не по арифметическому, а по логарифмическому правилу; для этого нужно воспользоваться таблицей, данной в Приложении 3. Таким образом, для перегородки площадью 4 м2 при уровне проходящей волны 50 дБ и частоте 100 Гц уровень мощности прошедшей волны будет равен 56 дБ (одно удвоение площади даст 3 дБ, второе— еще 3 дБ).

Теперь проделаем в стенке отверстие. Что произойдет? На рис. 43 дан график, позволяющий произвести расчет: исходя из относительной доли площади с низкой звукоизоляцией и площади с большой звукоизоляцией находят потерю изоляции перегородки, обусловленную «плохими» участками.

В качестве примера рассмотрим перегородку с трещиной у пола. Пусть площадь трещины составляет всего 1/500 часть площади перегородки, и пусть на частоте 4 кГц звукоизоляция перегородки равна 60 дБ. Согласно рис. 43, трещина снизит звукоизоляцию перегородки на целых 33 дБ! Отсюда ясно, как важно тщательно ликвидировать всякие трещины и зазоры во всех случаях, когда необходима хорошая звукоизоляция. Поразительно, как редко доходят до понимания этого обстоятельства! Ниже мы увидим, насколько важно герметизировать дверь по всему периметру. Кирпичные стены всегда следует штукатурить, чтобы не оставалось сквозных пор.

Рис. 43. Снижение изоляции при наличии участков малой изоляции на перегородке с большой звукоизоляцией
(множитель 1000 относится к правой половине рисунка).

Неблагоприятный эффект малых отверстий особенно сильно сказывается на высоких частотах. Волны отражаются от отверстий, малых по сравнению с длиной волны, а не проходят через них. Читателя это не должно удивлять: мы видели, что резонансы в трубе вызываются отражением волн от открытых концов. Здесь мы вновь сталкиваемся с различием импедансов: импеданс отверстия в стене выше, чем импеданс свободного воздуха. Поскольку же почти любая звукоизолирующая перегородка гораздо более эффективна на высоких, чем на низких частотах, утечка звука скажется более сильно на высоких частотах.

Для звука, прошедшего через отверстие средних размеров, характеристика направленности оказывается различной для высоких и низких частот — это обусловлено дифракцией и интерференцией. Пучок высокочастотного звука, исходящий из отверстия, направлен прямо перпендикулярно стене. Низкочастотный звук дифрагирует во все стороны, и его характеристика направленности больше похожа на полусферу.

Итак, подведем итоги тому, что мы узнали о звукоизоляции.

1. Для однослойной перегородки требуется высокая поверхностная плотность (например, кирпичная перегородка толщиной 230 мм имеет плотность 400 кг/м2).

Поскольку удвоение или уменьшение в два раза массы перегородки дает изменение ее звукоизолирующей способности всего на 4—5 дБ, оказывается, можно применять и перегородки с поверхностной плотностью всего 5 кг/м2, при условии что

2. упругость перегородки мала (за исключением случаев, когда требуется изолировать только низкие частоты, 30 Гц и ниже). При малой упругости резонансы колебаний и резонанс совпадений раздвигаются на края частотного диапазона, где эти явления обычно менее существенны. В противном случае следует иметь в виду, что резонансы и эффект совпадений значительно снижаются, если

3. перегородка сильно задемпфирована либо вследствие внутреннего трения в материале перегородки, либо в результате нанесения на ее поверхность слоя поглощающего материала.

4. Наилучшая звукоизоляция при заданном суммарном весе достигается путем применения двух или большего числа раздельных перегородок, связанных между собой возможно более податливыми связями. Звукоизоляция улучшается при увеличении воздушного промежутка между перегородками. Поскольку резонансы промежуточного воздушного объема могут снизить звукоизоляцию (в наихудшем случае двойная перегородка может оказаться хуже однослойной),

5. промежуточное пространство должно быть заполнено тем или иным звукопоглощающим веществом. В ряде случаев можно заставить поглотитель весьма эффективно выполнять вторую функцию — нести на себе вторую перегородку, как, например, в случае плавающих полов или листового материала с наклеенным на него слоем микропористой резины.

6. Эффект изоляции может оказаться катастрофически сниженным при наличии трещин, зазоров и отверстий, однако, как показывает рис. 43, и в случае, когда от участков с меньшей изоляцией освободиться нельзя, еще не все потеряно.

7. Нанесение на стены звукопоглощающих материалов, например пористых матов, само по себе не улучшает звукоизоляцию.

8. Звукоизолирующие перегородки и панели почти всегда создают большую изоляцию на высоких частотах и зачастую очень малую на низких.Частично это связано с законом масс (улучшение изоляции на 5 дБ при удвоении частоты), а частично с тем, что резонансы обычно имеют место на низких частотах. Поэтому выражение звукоизоляции перегородки каким-то одним числом децибел вводит в заблуждение, и весьма важно провести расчеты для всего диапазона интересующих нас частот. Для этого удобнее пользоваться октавными полосами частот (см. гл. 4). Иногда тем не менее оперируют некими усредненными величинами звукоизоляции, выраженными в децибелах, для всего диапазона частот от 100 до 3200 Гц.